Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 [ 25 ] 26 27 28 29 30 31 32 33 34 35

ций с малым коэффициентом заполнения, характерным для строительства последних лет, свидетельствуют о необходимости повышения аэродинамических коэффициентов. К таким сооружениям относятся башни с гибкими раскосами, когда основной наветренной площадью становятся пояса. В известной мере это относится и к мачтам, решетка которых выполнена из двух перекрещивающихся раскосов из круглой стали, что делают для снижения ветровой нагрузки.

Обычно наибольшая нагрузка бывает при ветре, направленном на угол решетчатой башни квадратного сечения - по диаго-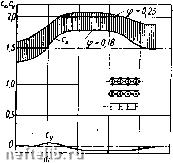

с.с,

70 30 40 d" Угол атаки

Рис. 3.42. Коэффициенты Сх л Су квадратного сечения ферм из круглой стали в зависимости от угла атаки (Re=118 000)

(? О? О J 0.1

Рис. 3.43. Коэффициенты c.v и cj, трехгранных ферм из стержней с острыми краями в зависимости от коэффициента заполнения грани

пали, в ряде случаев наибольшее давление иа нее может быть при ином направлении ветра, например под углом 30°.

На рис. 3.42 приведены коэффициенты лобового сопротивления квадратного сечения решетчатой конструкции, выполненной из круглой стали с шероховатостью ее поверхности kld = = 1-10- (=40 лк). Модели исследовались при числе Re = = 118000, отнесенном к диаметру пояса фермы (В. И. Ханжон-ков). Кризис у таких шероховатых стержней наступает раньше -при Re= (0,5-2) 10 Наибольшее значение конструкции наблюдается при угле а = 20-30°, а не при 45°, как это наиболее часто у ферм из угловой стали. Давление на пространственную, конструкцию из круглых стержней примерно в 2,1 раза больше давления на ее грань. Это относится к раскосным и безраскосным конструкциям с коэффициентом заполнения грани 0,18-0,24 и.с различными узловыми соединениями.

Исследование моделей четырехгранных решетчатых приз.м из круглой стали, на которых были установлены секции телевизионных антенн, выполненные из труб, выявили аналогичное

поведение конструкций (МГУ). Зависимость коэффициента лобового сопротивления от чисел Рейнольдса Re= (510) 10*, вычисленных по диаметру поясов модели, не обнаружена. Наибольшее значение коэффициента Сх наблюдается также при угле а = 20-:-30°, а не при а=45°. Коэффициент Сх квадратного сечения решетчатых призм на 20-30% больше коэффициента Сх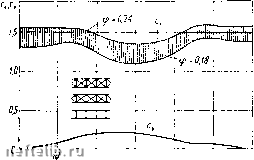

20 30 40 50

Рис. 3.44. Коэффициенты Сх к Су трехгранных ферм из круглой стали в зависимости от угла атаки (Re=118 000)

ОДИНОЧНОГО круглого цилиндра. Степень турбулентности аэродинамической трубы, где проводились эти измерения, е = 0,1%; она определена по шару (Re--=375000) известным способом.

Преимущества трех поясов в сечении вызвали появление . трехгранных башен и мачт. Наибольшая ветровая нагрузка на трехгранную решетчатую призму будет при ветре по нормали к грани, потому что в этом случае затенение задних стержней наименьшее (рис. 3.43). При ветре по биссектрисе угла и ветре, направленном параллельно одной из граней конструкции, нагрузка будет меньше, чем при направлении ветра на грань. Характерна значительная подъемная сила прп углах атаки а=30°, что учитывают в расчетах. Эти данные относятся к конструкциям из стержней с острыми краями (см. табл. 3.1).

Коэффициент лобового сопротивления трехгранных ферм из круглой стали, подобных четырехгранным, в условиях докризисного обтекания {Re= 1,18-10*) увеличивается примерно в 1,6 раза по сравнению с сопротивлением плоской фермы той же конструкции (рис. 3.44). Коэффициент заполнения грани этн.ч фep.г 0,18-0,24. Наибольшая величина коэффициента лобового сопротивления фермы остается примерно постоянной в пределах углов а = 0-15° и а = 45-60°, минимум коэффициента Сх наблюдается вблизи угла а = 30°, но в окрестности этого угла появляется значительная подъемная сила.

Ветровую нагрузку на решетчатые конструкции из труб или круглых стержней определяют по формуле (3.15). При осредне-

НИИ числа Рейнольдса по диаметру стержней фермы искажается представление о действительной картине обтекания: если число Рейнольдса вычислено по большому диаметру поясов, то обтекание решетки окажется также закризисным; на самом деле для меньшего диаметра решетки оно будет докризисное. Для таких конструкций тем более недопустимо относить число Рейнольдса к размеру поперечного сечения всей фермы.

Ветровую нагрузку на пространственную конструкцию с шестью гранями и более определяют, рассматривая ее состоящей из двух половин решетчатого многогранника. Нагрузку на наветренную ферму определяют как на условную плоскую ферму, являющуюся проекцией ферм на плоскость симметрии конструкции, т. е. учитывают углы наклона (скольжения) отдельных граней. При этом принимают во внимание удлинение граней, форму сечения стержней, коэффициент заполнения и число Рейнольдса- для круглых стержней. За расстояние между этими условными фермами принимают диаметр окружности, вписанной в многоугольник. Подветренную ферму учитывают коэффициентом ц. Расчетным случаем будет часто ветер, направленный па нормали к плоскости одной из граней, если конструкция - с четным числом граней, что встречается чаще.

Ветровую нагрузку на многогранную решетчатую конструкцию определяют, пользуясь данными о коэффициентах лобового сопротивления фермы при различных углах скольжени» (см. рис. 3.34 и 3.39), влияние подветренных ферм учитывают коэффициентом, например, по рис. 3.41.

При размещении на опоре технологического оборудования расчетной схемой будет наиболее неблагоприятное сочетание нагрузок на несущую конструкцию и оборудование, принимая при каждом направлении ветра свой коэффициенты лобового сопротивления, т. е. с учетом углов атаки и скольжения.

Коэффициент лобового сопротивления п одинаковых плоских решетчатых ферм, расположенных параллельно и на равном расстоянии друг от друга, определяют по формуле

спр = с*[1-}-(«-1)11], (3.20)

где с*-коэффициент лобового сопротивления одинарной фермы, в котором учтены особенности формы сечения и размеры стержней; т1 - принимается по рис. 3.41.

Расчетная ветровая нагрузка на пространственную конструкцию из многих параллельных ферм будет при направлении ветра под небольшими углами. Она на 10-20% больше, чем нагрузка по формуле (3.20).

Для определения ветровой нагрузки на пространственные решетчатые конструкции предложены различные формулы, в ко-

6-1138 81