Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 [ 18 ] 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57

малоугловой границы при пластической деформации. На рис. 55, а показана одна из таких границ наклона в кристалле, пунктир - след плоскости скольжения (базисной в г. п. решетке), по которой перемещаются дислокации при пластической деформации. Если в нижней части кристалла имеется препятствие и величина касательных напряжений в этой плоскости окажется достаточно большой, то произойдет разрыв дислокационной стенки (см. рис. 55, б), ее

рис. 55. Образование трещины в результате перерезания малоугловой границы при пластической деформации:

с -картина до деформации; б-схема зарождения трещины; в-трещина, образовавшаяся в цинке (Гилман)

концы разойдутся, а скачкообразно возникающая при этом растягивающая деформация может вызвать появление трещины. Картина, наблюдаемая в реальном кристалле цинка (см. рис, 55, в), очень близка к описанной схеме.

Часто зарождение трещин наблюдается в месте встречи двойника деформации с каким-либо прочным барьером, например границей зерна или другим двойником (рис. 56, а). Как известно, двойники распространяются с высокой скоростью, и возникающие при столкновении с препятствием напряжения не успевают релаксировать. Особенно благоприятные условия для зарождения трещин создаются при встрече растущего двойника деформации с ранее образовавшимся, для которого было характерно другое на-

правление двойникования (рис. 56, б), В этом случае концентрация напряжений в месте встречи особенно велика.

В условиях сильно развитой межзеренной деформации увеличивается вероятность зарождения трещин на границах перемещающихся один относительно другого кристаллитов. Рассмотрим стык трех зерен (рис. 57, а) в растягиваемом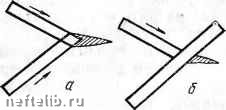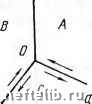

Рие. 56. Схема возникновения трещины при встрече развивающихся двойников {а) и торможения одного двойника другим (б)

Рис. 57. Схема зарождения трещины в стыке трех зерен за счет межзеренной деформации (Чэнг, Грант)

образце. Межзеренные смещения будут проходить в основном вдоль границ между зернами А-С и Б-С, где действуют большие касательные напряжения. В результате трещина зарождается вблизи места стыка О и распространяется вдоль границ Л-С и В~С (рис. 57, б). На практике с такой схемой зарождения трещин в результате меж-зеренных смещений встречаются обычно при высокотемпературных длительных испытаниях. В этих условиях возможно также зарождение пор (трещин) путем слияния вакансий (см. гл. VIII).

Рассмотренные основные схемы зарождения трещин показывают, что разрушение металлов с разной решеткой и микроструктурой может начинаться по-разному. Но в итоге сопротивляемость металла или сплава разрушению и характер разрушения определяются условиями, в которых оказывается возникшая по тому или иному механизму микротрещина. Вторая стадия разрушения - распространение трещины - является решающей.

3. Развитие трещины с позиций механики разрушения

Современный анализ развития трещины базируется на концепциях механики разрушения, исходящей из того, что макроскопическое разрушение тела (образца или конструкции) является результатом развития трещин, которые возникают либо в процессе его изготовления, либо как результат деформации во время испытания образца или эк-

сплуатации детали. Учитывая наличие трещин, механика разрушения устанавливает количественную связь между действующим на тело напряжением, формой и размерами трещин и сопротивлением материала докритнческому (стабильному) н закритическому (нестабильному) развитию этих трещий.

Современная механика разрушения является развитием известной теории хрупкого разрушения Гриффитса. Он исходил из того, Что в материале всегда имеются уже готовые трещины, и проанализировал условия, при которых эти трещины будут развиваться как хрупкие, т. е. нестабильно, с большой скоростью.

в теории Грнффитса и в механике разрушения обычно рассматривается растягиваемая изотропная бесконечная пластина конечной толщины в которой имеется эллиптическая трещина с радиусом закругления г, стремящимся к нулю (рис. 58). Если длина 2с значительно меньше ширины а. Любая трещина действует как концентратор напряжений. У вершины трещины возникает максимальное напряжение Sm-=2S{clryf\ где 5 -приложенное извне напряжение. Из этого уравнения Инглиса следует, что при одном и том же внешнем напрялсении у вершины трещины будут возникать напряжения, тем ббльщие, чем она длиннее и острее. При определенных значениях 5, с и г напряжение Sm превзойдет теоретическое сопротивление отрыву Sot, мбжатомные связи у вершины трещины разорвутся, и трещина начнет развиваться. Если рассматривать, как Гриффите, идеально хрупкое тело, в котором пластическая деформация у вершины трещины не проходит, то при распространении трещины будет выделяться энергия упругой деформации, но, с другой стороны, должна затрачиваться работа на создание увеличивающейся поверхности трещины.

При растяжении тонкой пластины единичной толщины у вершины эллиптической трещины возникает плоское на-

рис, 58. Пластина с трещиной в условиях растяжения

пряженное состояние, и в этом случае упругая энергия, выделяющаяся при росте трещины, будет равна Ue :==-TicS/E а затрачиваемая поверхностная энергия Us = .=4cys, где Ys - удельная поверхностная энергия стенок трещины. Трещина будет распространяться при условии, что увеличение поверхностной энергии будет полностью компенсироваться выделением энергии упругой деформации. Иными словами, условием развития трещины является неизменность общей энергии системы при любом малом приращении ее длины

dU/dc =d(U-\- U]/dc - (- 2пс5УЕ) + 0. (39)

Отсюда получаем известный критерий Гриффитса

S.y2EyJ(nch (40)

определяющий величину внешнего напряжения S, при котором трещина длиной 2 с начнет развиваться как хрупкая. Критерий Гриффитса позволяет определить критическую длину трещины, которая будет распространяться при действии на тело (вдали от нее) заданного напряжения S.

Если растягиваемая пластина (см. рис. 58) имеет достаточно большую толщину, у вершины трещины возникает объемное напряженное состояние трехосного растяжения (и соответствующее ему плоское деформированное состояние). Для этого случая критерий Гриффитса записывается в иной форме:

SV2EyJ[(i-v)h (41)

где V - коэффициент Пуассона.

По уравнениям (40) и (41) напряжение обратно пропорционально корню квадратному из длины трещины. Следовательно, при развитии трещины по мере увеличения ее длины необходимое для этого напряжение должно снижаться. Значит, рассматриваемый процесс развития хрупкой трещины должен быть самоускоряющимся. Скорость этого развития быстро возрастает до предельной величины, достигающей, как уже отмечалось, того же порядка, что скоросгъ распространения звука в данном материале.

При выводе критерия Грнффитса использовались допущения, неприемлемые с точки зрения современных представлений о разрущении металлов. Главное, что вызывает возражения, - это игнорирование пластической деформации, хотя бы локальной, до и во время развития трещины. На самом деле такая пластическая деформация в металлах

всегда предшествует зарождению трещины и проходит в более или менее узкой зоне у вершины трещины, где напряжения превышают необходимые для начала пластической деформации. Таким образом, поскольку в металлических материалах невозможно идеально хрупкое разрушение, критерий Гриффитса требует изменений.

Простейшим из них является замена ys на у = у8+7пл, где 7пл - работа пластической деформации, которая затрачивается на рост трещины. Эта замена возможна, если пластическая деформация концентрируется в зоне перед вершиной трещины, ширина которой мала по сравнению с длиной трещины. В таком случае мы имеем дело с макрохруп-ким разрушением, достаточно частым в металлических материалах. При этом в большинстве случаев уилОУз, и критерий Гриффитса для металлов можно приближенно записать как

Таким образом, при распространении хрупкой трещины в металлах должно соблюдаться равенство выделяющейся энергии упругой деформации и работы пластической деформации. Поскольку упл значительно больше Vs, критическая длина трещин в хрупких металлах имеет величину порядка миллиметров, в то время как в истинно хрупких материалах, например стекле, - микрометры.

Ирвин ввел параметр

(42)

который, как видно из уравнения (39), является первой производной упругой энергии, выделяющейся при раскрытии трещины, по длине трещины. Он назвал его сопротивлением продвижению трещины. Действительно, физический смысл параметра G состоит в том, что он характеризует работу, которую надо затратить на образоваппе новой поверхности трещины единичной длины нли переместить фронт трещины единичной длины на единичное расстояние. В металлах

пл

(43)

Параметр G, прямо связанный с теорией Гриффитса, является энергетическим критерием сопротивления развитию трещины. Еще шире используется силовой критерий, который можно получить, зная ноле напряжений у фронта трещины. Допустив линейную связь напряжения с деформацией, можно следующим образом выразить компоненты

тензора напряжений, действующие на элементарный параллелепипед, расположенный иа расстоянии / от фронта трещины, еслн / образует с осью х угол ф;

S (пс) ,,„;очг1 sjj cos (Зф/2)];

- V (5, + 5,);

cos (ф/2)[1 cos (ф/2.)[1

5ш(ф/2) 5Ш(Зф/2)];

(44)

(2яг)

sin (ф/2) cos (ф/2) cos (Зф/2);

уравнения (44) дают хорошее приближение в области, где величина / мала по сравнению с длиной трещины и размерами пластины. Поэтому механику разрушения, рассматривающую поле напряжений в этой узкой области, называют линейной. Формулы линейной механики разрушения (44) неприменимы при /=0, так как в этом случае дают бессмысленный результат - бесконечно большие значения напряжений.

В зависимости от толщины растягиваемой пластины у вершины трещины реализуются, как уже отмечалось, различные виды напряженного состояния. Если пластина достаточно толстая и возникает плоское деформированное состояние, то поперечной деформации вдоль оси z не будет. Образующееся в тонкой пластине плоское напряженное состояние характеризуется равенством 5=0. Силовой критерий разрушения, МПа-м

/С = 5 (ncf . (45)

Легко показать, учитывая уравнение (42), что он связан с энергетическим критерием: GK-jE (46).

Не зависящий от положения в полярных координатах / и ф параметр К называется коэффициентом интенсивности напряэюений. Он характеризует локальное повышение уровня растягивающих напряжений у вершины трещины. Несмотря на необычную размерность, МПа-м*, коэффициент К молсет быть интерпретирован как напряжение, действующее впереди вершины трещины вдоль направления ее распространения на расстоянии 72л, мм, от вершины. Дру-

1 МПа.м«3,Ш кгс/м.м-