Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 [ 7 ] 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56

в диапазоне перемещении от 1 до 6 см (прн трубах диаметром до 529 мм}. Для этого диапазона перемещсинн зависимость близка к лниснной. При аппрокснманпн полученных кривых лннеГшоп функцией можно отметить, что коэффициент нормального сонротпвлення /рунта. равный тангенсу угла наклона прямой, тем меньше, чем больше диаметр трубы, что соответствует физической сущпостп яв.чсння.

На основании проведенных экспериментов обобщенный коэффициент порма.тьного сопротивления грунта рекомендуется вычпсяять по формуле

/ J!Ll.\

(3.34)j

Коэффициент пгиг определяется в зависимости от отношения расстояния От боковой образующей трубы до стенки траншеи а к расстоянию от осн,трубы до верха засыпкн ftn-

На рис. 12 приведен полученный на основе обработки экспериментальных данных в соответствии с формулой (3.34) график для опрсдсяення] коэффициента Цгор.

Как следует из графика, прн с=0 (прилегание трубы вплотную к стенке Tpannien) коэффициент т]гор=0,93, т. е. зависимости (3.24) и (3.34) практически совпадают.

Принципиальным от.тнчнем моделей грунта при поперечных перемещениях трубы в горизонтальной (в плане) и вертикальной (вверх) плоско-стя.ч, несмотря иа аналогию формул (3.24) и (3.34), яв.чяется то, что при поперечных персмеп;сиия.\ в плане линейная завпсимость реализуется при значительных нсрсменгепнях трубы, составляющих примерно 0,1 диаметра трубы. Однако прн расчетах трубопровода, прокладываемого в мабых грунтах, в некоторых случаях поперечные перемещения могут быть н более указанного зиачспия. Для таких случаев можно предложить ,чва вида нелинейных моделей (рис. 13).

Первый вид модели (рис. 13, а) соответствует условиям прокладки, когда предельная удерживающая способность грунта больше его условной

несущей способности (пр. rnp>/?l-p/B,i).

Под преде.тьной удерживающей способностью грунта qnp гор понимается пре.чельнос сопротивлспне грунта перемещениям трубы в горизонтальной плоскости, определяемое также как пассивное боковое давление грунта при расчетах подпорной стенки:

-Jnp.ropYrpWp.

(3.35)

Рис. 12. График для онрсделепня коэффициента Цгор

Рпс. 13. Диаграммы сопротивления грунта поперечным горизонтальным перемещениям трубы

},,5фф11инс11т пассипного бокового давления определяется но формуле

(tg45 -h-Prp/S), (3.36)

ftp -tgM45 , Фгр/2)

VVpn

-сцеплснпе грунта; у.-р -

где гр -угол кнутрсниего трения грунта; Сгр-п.--ьемпый вес грунта.

Под несущей способностью грунга Ягр понимается критическое значе-ннс среднего давления, которое приведено в нормах иа проектирование пснопаний и фундаментов.

Второй вид модели (рис. 13,6) соответствует условиям прокладки, когяа QP Tvp<RvflD„- В этом случае при больших перемещениях ие происходит выхода линий скольжения на поверхность, и сопротивление грунта псремсшонню трубы не изменяется.

ГЛАВА 4

ПРОДОЛЬНЫЕ ПЕРЕМЕЩЕНИЯ ПОДЗЕМНОГО ГРУБОПРОвОДА

Изменение температурного перепада и внутреннего давления в подзем ном трубопроводе вызывает в нем продольные напряжения. Величина эти напрялсений зависит от псремещепий трубопровода, которые в общем слу Чае могут иметь место при изменении копструктивпы.ч пара.мегров тр\бо провода: непрямолииейности первоначальной осн. при нере.х.оде от иодзем кой прок.тадки к открытой, при разности величин воздействий (темпера турного перепада и впутреннего давления), при изменении геометрпч! ских характеристик трубы (диаметра и толщины стенкп) или при на.чнчи упругих Связей но коицам трубопровода.

§ 1. Общее решение для определения перемещений и усилий при продольных перемещениях

Рассмотрим ирямолннейпый подземный участок трубопровода, правыГ конец которого иенодвижен. Для общности решения будем считать, что трубопровод имеет ограниченную длину L.

За начальный параметр принимаем осевое усилие Ло, остальные обо значения показаны па рис. 14.

В качестве расченю!! модели трубопровода нсцользуем стержень (балку трубчатого сечения, взанмодействуюншп со средой. Взаи.модействие трубо Провода с грунтом описывается зависимостью сопротивления грунта от пе ремещения, диаграмма приведена на рис 1.5, а. Она учитывает ограничен пость по величине реакций продольных связей. .Аналитическое выражение модели грунга. представленной на этой диаграмме, имеет пнд:

tx--~ -пРцСхоПх при \ttxl-

t = t„p, при Hjfl>

(4.1

Здесь fx - сопротивление грунта продольным перемещениям трубы; Ск о - коэффициент пропорциональности, называемый обобщенным коэффициентом касательного сопротивления грунта.

В зависимости от нагрузок, воздействий н относительной жесткости трубопровода возможно, что на всей длине рассматриваемого участка грунт работает только я упругой стадии, характеризуемой условием (4.1), либо на этом отрезке имеют место два участка, описываемых условиями (4.1 и (4.2).

Участок, где взаимодействие трубопровода с грунтом описывается з Бисимостью (4.2). на:1овем участком предельного равновесия, а его длин; обозначим через Lj,, в да.чьиейщем будем называть его просто исрвы: участком.

Уравнение равновесия элемента dx (см. рис. 15,6) имеет вид

dNx!dx+tx==Q. (4.3)1

С учетом (4.1) и (4.2) для каждого из участков это уравпение запишется так:

rfArdA--bip = 0. при \Ux\>

nD»Cx а

(4.4)

dSndx ~ ziDnCx о = 0. при

ПОцСх о

Cool ношение тсрмоупругосгп, ..чигывая двухосное напряженное со-ггопиис напорного трубопровода.

0. о

сголиис имеет ВИД

(4.6)

Рис. 14. Расчетная схема подземпого участка трубопровода

Здесь Сх - продольная деформация; £ -модуль упругости материала; г-ппощадь сечения стенок трубы; а - коэффициент линейного pacuuipe 1ШЯ- \f температурный перепад, положительный при нагревании; ji -коэффициент П>ассоиа, о„ц - кольцевые напряжения от внутреннего дав-iCII И и

в линейной постановке задачи деформации и перемещения связаны за-ппсимостью

Тогда

NxEF

Вх ~ dii dx. du

- (аМЕ - (хокц) F.

(4.7) (4.8)

Нспачьзля (4.8) и считая, что сечение трубопровода, температурный

перепад и виутреинее дав.ченне будут постоянны.ми по дллие, уравнения равновесия (4.4) и (4.5) в перемещениях имеют вид:

dhiildx + t„j,EF=0; (4.9)

duiidx , l*wn=--0. (4.10)

ynDCxoEF. (4.11)

Запишем решение уравнений (4.9) и (4.10) оттсятелъио псреешсиш и усилий:

«.=-(---l-C->+C.); V4.12)

Л. = - яр* + с, - (аЫЕ ,ло, f: (4.13)

Cg sh ух ch ух: (4.14)

EFy (Cg ch ух -1- sh ух) - (аМЕ - цоц) F. (4.15)

.V„ =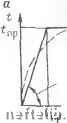

dx

агщжпсд

Рис. 15. Расчетная модель грунта и элемент трубопровода

Считаем, что параметры трубопровода таковы, что по длине труби провода имеется участок предельного равповесяя грунта. Тогда гранич ные условия п условия сопряжения обоих участков в данной иостаноп< задачи имеют вид:

прн хО при x = J,p Hi = «,i, Ai = Af,j,

"х = - "np--fnpf"»x о- "РИ = "и = 0- 16)

Исходя из этих условий, определяем произволы1ые постоянные Cj-Ci ypaBHeinn"i (4.12)-(4.15) и длину участка предельного равновесия-

1 -.

С прпр

PJiP V "~i.p)

"U\p-thTsh7,;j

пр / Сд -Csthl.

(4.17)

othoSZZt: """""" трансцендентному уравнению, ре.пая его

l-thLth%,

:з г---г- 1„р ~ N.

Здесь введены следующие безразмерные параметры:

(4.18,

(4.19),

Лfo, = (-aД£-LOкц). (4.20)1

Определив из уравнения (4.18) lap. по формулам (4.17) находим про-, извольпые постоянные, которые позволяют с помощью уравпеций (4.12) - (4.15) определить перемещение и продатьиое усилие любого сечения трубопровода.

Запишем значение продольного перемещения и продольного услдия соответственно в начале н конце участка трубопровода:

M„ = C,/£f: (4.21)

ch*L

(4.22)

пр = Л-1, /„р =

(4.23)

Произвольные постоянные в этом случае записываются в виде

2прТ

ffye-vfnp

(4.24)

Тогда перемещение в начале участка будет 1

«0 =

(4.25)

Усилие в «защемленной» части трубопровода, где перемещение равно нулю, составит

NlN:. (~a.ME-\-v.a)F. (4.26).

Для опенки размера участка, который можно принять за бесконечно длштый, npHiUew условие, что перемещение его правого конна равно 1 % от псрсмещсипя, соответствующего перемещению конца участка предельного равновесия, т. с.

Н£.-0.01н„р -0,01

Из (4.12) с учетом (4.27) по-чучн-м уравнение дтя L

(4.27)

(4.28)

По этой формуле можно определять длину участка трубопровода, с которого «собираются» перемещения к его началу.

Изложенное относится к случаю, когда по длине трубопровода Hiic-ются два участка: участок предельного равновесия грунта /и,,, где сянро тивление но длине постоянно и равно tup. к участок упругой работы грунта, где сопротивление грунта пронорцнонально персмен;снию. Критерий наличия участка предельного равновесия грунта можно получить из (4.18), считая, что /п1..>0. Тогда указанный критерий можно записать в виде

N thL> I.

Дли нолубескопечного участка этот критерий будет иметь вид (JV,-A.)T пр

> 1.

(4.29)

(4.30)

Теперь рассмотрим случай, когда участок предельного равновесии отсутствует, т. е. когда критерии (4.29) и (4 30) не выполняются. Как и ранее, рассматриваем в качестве начального парамегра (прн х=0} продольное усилие Ло.

Уравнение, оппсывающее изл1снеине продольных перемещений и продольных усилий по длине трубопровода, записывается аналогично (4.14). (4.1о).

Ux г?1 sh п + А ch ух; (4.31)

Nx = EFy (D, ch ух + D, sh ух) - {аМЕ - (Шкц) Р. (4.32)

Произвольные постоянные Di к определяем из граничных условий:

при = О, Nx Nn, при л; = L, = 0. (4.33)

Продольное перемещение и продольное уснлне соответственно в начале « конце участка трубопровода будет

Мо= -

Л +

Л- -Л

chvL

(4.34)

(4.35) 49