Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 [ 7 ] 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121

мации у стенки трубопровода при течении по нему ньютоновских жидкостей:

Формула, описывающая взаимосвязь между Sv/de и (-dv/dr)ст, была получена Рабиновичем и Муни. Метцнер и Рид в 1955 г. представили эту формулу в виде

\ dr let \ /

Подставляя выражение для (-dv/dr) в уравнение (1.3-2), получим

(1.3-12)

(-J. (1.3-13)

Для ламинарного течения в горизонтальном трубопроводе по уравнениям (1.1-1) -(1.1-3) определяем Непс-пл примем v = v. Используя уравнения

т=, (1.3-14)

v=-. (1.3-15)

а также уравнения (1.3-2) и (1.3-11) для течения псевдопластиков, можем написать выражение для обобщенного числа Рейнольдса, выведенное Метцнером и Ридом

dl t»<2-«) 8

Ке„е.пл= (6-f2/n)« (1.3-16)

С учетом данных проведенных расчетов можно считать, что уравнение (1.3-15) действительно для псевдопластичных жидкостей, подчиняющихся степенному закону; при этом р, и и - постоянные, численные значения которых заданы уравнением реологической кривой. Заменяя ii в уравнении (1.3-15) выражением (1.3-13), получим:

Ке„е.ил=:. (1.3-17)

Эта формула используется в случае, если реологические свойства жидкости определяются капиллярным вискозиметром или при полевых

испытаниях на трубопроводе, либо по кривой Тст = /(8и/а!в). В соответствии с уравнением (1.3-12)

если жидкость подчиняется степенному закону, то k и п - постоянны и их численные значения известны. Однако эту формулу можно ис-

пользовать и в случае, если свойства жидкости отклоняются от степенного закона, для чего достаточно предположить, что уравнение (1.3-12) представляет собой уравнение касательной к кривой Тст = /(8ц/в), построенной в ортогональной билогарифмической cncfcMC координат; п - крутизна кривой, а k - ордината при (8у/с(в) = 1. Касательная должна касаться кривой в точке, абсцисса которой (Sv/cIe) соответствует фактическим величинам q и da- Если движение потока характеризуется кривой Тст = /(8о/в), то выражение для обобщенного числа Рейнольдса можно получить более просто, исходя из последующих рассуждений (ЛеБарон Боуен, 1961).

Используя уравнения (1.1-1) - (11-3) и выражение v=ip/p, можно написать

0,2МвАр

Подставляя это выражение в уравнение (1.1-2), найдем

Re= i. (1.3-18)

Это выражение действительно для всех неньютоновских жидкостей, включая псевдопластичные, отклоняющиеся от степенного закона, для которых, очевидно, Re = Renc. пл. Чтобы найти по этому уравнению число Рейнольдса, необходимо рассчитать Тст в соответствии со значениями V и dn, снятыми с экспериментально построенной кривой Тст - = /(8и/й(в), и подставить полученное значение в формулу (1.3-18).

1.3.4. ПЕРЕХОД ОТ ЛАМИНАРНОГО РЕЖИМА К ТУРБУЛЕНТНОМУ

Переход неньютоновских жидкостей от ламинарного течения к турбулентному определяется, кроме числа Рейнольдса, рядом других факторов, зависящих от реологических свойств данной жидкости. До настоящего времени не предложено формулы для расчета переходной зоны, однако отдельные исследователи опубликовали достаточно ценные результаты частичных исследований проблемы. Райян и Джонсон предложили параметр устойчивости потока, который позволил выразить критическое число Рейнольдса псевдопластичных жидкостей, подчиняющихся степенному закону, следующим образом:

Ре в"кр~" 3 6464

Кепспл.кр- . Р (6 + 2/п)« ~ ф (п) • (1.й-1У>

п + 2

. (1.3-20)

Приняв для ньютоновских жидкостей Рекр=2100, можно определить, что критическое число Рейнольдса для псевдопластичных жид-

3* 35

костей в зависимости от экспоненты степенного закона колеблется в пределах 2100-2400 (Говье и Азиз, 1972).

Додж и Метцнер в 1959 г. нашли, что Rcnc. пл. кр в некоторой степени уменьшается по мере уменьшения п. По расчетам этих авторов, Rene. пл.кр=3100 при R = 0,38.

10 •

du/d, с"

Рис. 1.3-7. Области ла.чинарного и турбулентного течения в трубопроводах по ЛеБарон Боуену (1961).

л - область ламинарного течения независимо от диаметра трубопровода: В - область турбулентного течения при диаметре трубопровода (в мм): / - 400; 2 - 200; 3 - 100; 4 - 50; 5 - 25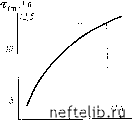

10 20

Рис. 1.3-8. Экспериментально построенная зависимость предельного напряжения сдвига у стенки трубы от отношения 8 vlds

По данным Мирзаджанзаде и др. (1969 г.), переход к турбулентному режиму в значительной степени зависит от размера частиц и концентрации дисперсной фазы, а также от разницы плотностей дисперсной среды и дисперсной фазы.

Так как установленные до сих пор математические критерии пока еще далеки от определенности, целесообразно в сомнительных случаях экспериментально определять тип потока, преобладающего при данных условиях. Графики на рис. 1.3-7 определены экспериментально (ЛеБарон Боуен, 1961). Кривая А характеризует ламинарный поток независимо от диаметра трубопровода. Группа линий В представляет собой комплекс кривых, характеризующих турбулентный режим в трубопроводах различного диаметра. Чем меньше диаметр, тем больше абсцисса

(Sv/de), при которой поток становится турбулентным.

1.3.5. РАСЧЕТ ПОТЕРЬ НА ТРЕНИЕ

а) Ламинарное течение псевдопластичных жидкостей

По уравнению (1.3-12) напряжение сдвига, действующее у стенки трубы в жидкости при данных значениях /г и п, является функцией только Ву/в. Это позволяет непосредственно рассчитать потери на трение в трубопроводе любого другого диаметра, если известны экспериментальные данные, полученные при измерении капиллярным вискозиметром либо данные испытаний непосредственно на трубопроводе.