Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 [ 27 ] 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63

где Ибезд - коэффициент запаса несущей способности бездефектной трубы.

Подставив (6.64) в (6.59), получим характеристику безопасности

>«безд

-1/ безд (q)2

(6.65)

-1- 0)2 + 0)2 ) + со

Из (6.65) следует, что при й = Ибсзд вероятность разрушения будет 0,5. Это указывает на необходимость учета концентрации напряжений в местах дефектов; поэтому зависимость (6.65) является характеристикой для оценки опасности дефекта при действии внутреннего давления.

Вероятность разрушения при наличии дефекта определяется так же, как и для бездефектной трубы, но в качестве коэффициентов запаса и безопасности следует принимать

безд

И 7д = 7безд(-).

(6.66)

При этом можно для определения вероятности разрушения дефектного трубопровода Рразр пользоваться графиком, приведенным на рис. 6.15, на котором приняты обозначения Ибезд = х,

Убезд = Т-

§ 6.9. МЕТОДИКА РАСЧЕТА ПРОЧНОСТИ ТРУБОПРОВОДА ПО ЗАДАННОЙ МЕРЕ НАДЕЖНОСТИ

Основной подход к проблеме прочности, как к оптимизационной задаче, требует разработки метода расчета прочности по заданной мере надежности.

Приведенные в предыдущих параграфах результаты являются отправным материалом, который позволяет обосновать методику расчета прочности по заданной вероятности неразрушения.

1. Определение вероятности разрушения для участка трубопровода с одинаковыми условиями работы

Поскольку такой участок представляет систему последовательно соединенных труб, работающих в одинаковых условиях, то вероятность неразрушения системы определяется условием

(6.67)

Р(Г) = (1-Рр,зр)",

где Рразр - вероятность разрушения одной трубы, имеющей определенный набор дефектов, п - число последовательно соединенных элементов.

Из (6.67) следует, что вероятность разрушения

Рразр l-iTT-

Разложив в ряд Тейлора выражение (6.68), получим

разр

:-[1-Р(Л1+Г---)[i-P4T)] +

п 2 \п J

(6.68)

(6.69)

Определив по формуле (6.69) Р разр, ПО графику зависимости параметра безотказности у от Рразр (рис. 6.18) находим допустимое удоп (при полученном или заданном значении Рразр), которое определяет допустимое отношение Ибсзд/й- Приведем пример расчета участка трубопровода длиной 40 км. При средней длине трубы 12 м общее их число составит п = 3,310. Пусть нас интересует вероятность разрушения труб при мере надежности участка в целом Pi(r)=0,99 и Р2(Г) =0,999. Выполнив вычисления по (6.69), получим в первом случае Ppaзp3•10~

а во втором Рразр=3- 10-*.

Поскольку трубопровод не может проходить на всем протяжении по участку одной категории, то условие (6.69) можно использовать для оценки вероятности разрушения на каждом участке, характеризующемся одинаковыми условиями.

Рассмотрим трубопровод как систему последовательно соединенных элементов, представляюп;их отдельные участки, вероятность разрушения которых определена по формуле (6.69). Решение выполняется аналогично рассмотренному случаю с одним участком. Задаваясь требуемым значением меры надежности трубопровода в целом Р(ЁГ), определим по (6.69) вероятность его разрушения:

Рр.,р(Щ-[1-р{т)]+и+)1\-р{т)]+ ....

п 2 \ п /

(6.70)

где п - число отдельных участков с одинаковыми условиями работы труб.

Так же, как и для одного участка, для всего трубопровода в целом можно использовать график, представленный иа рис. 6.18.

2. Связь внутреннего давления в трубопроводе с мерой и аде л< ноет и

Основной нагрузкой для трубопровода является внутреннее давление, в результате действия которого в бездефектной трубе возникают соответствующие нормальные кольцевые напряжения акц. н. В дефектных .местах эти напряжения увеличиваются до

Окц. д =ЙОГкц. и, (6.71)

где k - коэффициент концентрации напряжений.

Труба начинает разрушаться, если

(6.72)

Допустим, что по всей длине трубопровода или его участка создано одинаковое внутреннее давление р. Поскольку дефекты по длине трубопровода будут различными, то в соответствующих местах расположения дефектов будут различными и значения характеристик безопасности у.

Если мы хотим обеспечить одинаковый уровень надежности участка трубопровода или в целом всего трубопровода, то необходимо, чтобы было выполнено условие

(6.73)

где Р(Т)-заданный уровень или мера надежности участка, а Удоп[Р(7")] - соответствующая этому уровню характеристика безопасности.

При этом на коэффициент концентрации k налагается ограничение

><беэд

(6.74)

•доп

где ибезд - запас несущей способности бездефектной трубы, Ядоп - запас несущей способности, соответствующий заданной характеристике безопасности уц,ои[Р(Т)].

Количественно Хбезд характеризуется отношением

- вр безд - = •

<Ткц. ii

3десь авр - математическое ожидание предела прочности, а акц. н - кольцевых напряжений в бездефектной трубе. Запишем Ибезд В виде

Ябезд - -<Тт

<Ткц. и

(6.75)

где ат - математическое ожидание предела текучести; - запас несущей способности материала по пределу текучести, т - запас несущей способности по внутреннему рабочему давлению Рраб в трубе, характеризующий уменьшение внутреннего давления по сравнению с тем, которое могла бы выдержать бездефектная труба.

При этом неравенство (6.74) будет иметь вид

(6.76)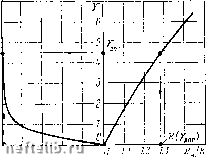

РтаЗ 0:8 С.7 0,6 0.5

Рис. 6.23. График зависимости меры надежности Р(Г) н характеристики безопасности у от условного коэффициента запаса Хн прн наличии концентраторов напряжений

Из этой зависимости можно сделать вывод о том, что допустимый коэффициент концентрации й=йдоп изменяется при изменении параметров, т. е. характеристик материала труб и меры надежности. Так, если запас по пределу текучести одинаков (одинаковые трубы), а Идоп задана для данного участка или трубопровода в целом, то йдоп линейно зависит от т.

Для облегчения вычислений в соответствии с изложенным на рис. 6.23 приведен график зависимости меры надежности

(7") и характеристики безопасности трубопровода у от коэффициента запаса несущей способности при бездефектных трубах Хбезд с учетом коэффициента концентрации напряжений k.

Допустим, задано Р(Г)=0,99. По графику находим удоп= = 4,5, а Идоп1,28; если принять Р(Г)=0,9, то достаточно выполнить условие идоп1,05.

§ 6.10. РАСЧЕТ ПРОЧНОСТИ УЧАСТКА ТРУБОПРОВОДА

Необходимо определить толщину стенки труб на участке длиной L = 48 км. На всем протяжении участка трубопровод находится в одинаковой среде, и каждая труба, входящая в состав участка испытывает одинаковое с другими внешнее силовое воздействие; напряженное состояние всех труб одинаково. Если это не так, то необходимо участок L разбить на ряд меньших участков таким образом, чтобы в пределах каждого из них напряженное состояние было одинаковым. В данном примере мы будем считать, что участок L находится на всем протяжении в одинаковых условиях.

Примем далее несколько ограничивающих допущений: трубопровод располагается в плотном грунте, на равнинной местности, уложен прямолинейно, продольная устойчивость трубопровода обеспечена.

Исходные данные: условный внутренний диаметр труб 120 см; средняя длина одной трубы 12 м; прочностные xapaKTcpncjHKH металла труб, определенные по испытаниям образцов, авр= = 5,77-10* Н/см ат = 3,8-10* Н/см; внутреннее давление продукта в трубопроводе р = 7,5 МПа = 750 Н/см.

Выполним вначале расчет прочности в предположении, что трубопровод не имеет дефектов. Расчет проведем для четырех

вероятностей неразрушимости труб: Р(Г) =0,95; 0,99; 0,999 и 0,9999. Для обеспечения прочности труб с заданными вероятностями неразрушимости кольцевые напряжения в стенке труб не должны быть больше определяемых по формуле (6.57)

Окц =feoflHVaBp.

В соответствии с рекомендацией § 6.6 масштабный коэффициент принимаем v = 0,85, а коэффициенты однородности одн определяем по формуле (6.53)

= 1-

вр-

Значения fe приведены на с. 158, а коэффициент изменчивости coogp прочности образцов берем из табл. 6.9: соовр = 0.042.

Далее по формуле (6.53) находим для различных Р{Т) коэффициенты однородности:

%одн (0,95) = 1 - 1 • 0,042 =-- 0,958;

йодн (0,99) = 1-2,33-0,042 = 0,903; ;од„ (0,999) = 1 - 3,1 • 0,042 = 0,870; ko„ (0,9999) = 1 - 3,72 - 0,042 = 0,844.

По формуле (6.57) для различных (7") находим:

акц (0,95) = 0,958-0,85• 5,77• 10* = 4,7-10* Н/см;

(0,99) = 0,903-0,85•5,77-10* = 4,4-10* Н/см;

акц (0,999) = 0,87-0,85-5,77• 10* = 4,26-10* Н/см;

акц (0,9999) = 0,844-0,85-5,77-10* =--4,14-10* H/cм

Толщину стенки трубы определим в соответствии с предложением, сделанным в работе [1], по формуле

Риспян

2акц

где р„(,п - испытательное давление, принимаемое р„сп=1,3 ррао (см. гл. 7). В рассматриваемом случае рисп= 1,3-750 = 975 И/см~. Определяем толщину стенки труб для различных вероятностей неразрушимости:

аналогично вычисляем б (0,99) = 1,32 см; б (0,999) = 1,37 см; б (0,9999) = 1,41 см.

Изменение меры надежности от 0,95 до 0,9999 приводит к увеличению толщины стенки бездефектной трубы на 1,7 мм. Поскольку этн толщины стенки рассчитаны на испытательное

давление, то кольцевые напряжения при рабочем давлении будут ниже тех, которые определены выше, а именно

Окц (0,95) =

рРвн 750-120 26i ~ 2-1,24

-"-3,63-10* Н/см;

а„ц(0,99)=3,41 • 10* Н/см2; анц(0,999) =3,28 • 10* Н/см; и аь-„(0,9999)=3,19- 10* Н/см.

Определим далее коэффициент запаса и несущей способности труб прн испытании из условия и = а11р/акц. При различных вероятностях Р{Т) коэффициенты запаса и= (0,95) = 1,22; и(0,99) = 1,3; х(0,999) = 1,35 и и(0,9999) = 1,40. По рабочему давлению запас несущей способности составляет и= (0,95) = = 1,59; и(0,99) = 1,69; и(0,999) = 1,73; и(0,9999) = 1,81. Характеристики безопасности у бездефектного трубопровода найдем по формуле (6.59) или по графику рис. 6.18. Соответствующие ее значения у(0,95) =3,4; у(0,99) =4,6; у(0,999) =5,2 и у(0,9999) = = 6. Как видно из этих значений, характеристики безопасности очень велики. Достаточно сказать, что у=3 обеспечивает практическую неразрушимость бездефектной трубы даже при толщине стенки 1,24 см, не говоря уже о толщинах 1,37; 1,32 и 1,41 см.

Рассмотрим далее влияние концентраторов напряжений на несущую способность трубопроводов с толщинами стенки труб, определенными выше.

Коэффициент концентрации напряжений определяем по формуле (6.63)

Допустим, что в качестве концентратора напряжений рассматриваются продольные заводские сварные швы или иные дефекты, которые создают концентрацию напряжений на уровне, определяемом в соответствии с данными § 6,7 коэффициентом концентрации k=l,3. Тогда коэффициенты запаса несущей способности с учетом дефектов определим по формуле (6.64).

бсзд

Выполнив вычисления, получим для труб с толщиной стенки 1,24; 1,32; 1,37; 1,41 см: Хд(б = 1,24) =0,938, Хд(б= 1,32) = 1,0; у.д(б= 1,37) = 1,038 и ид(б= 1,41) = 1,076. Воспользовавшись графиком рис. 6.27, определим по этим Ид меру надежностн дефектных труб Р(Т) и характеристику их безопасности у: при Хд=1 у = 0 и Р(7)=0,5; при Ид= 1,038 у=0,75 и Р(7)=0,8; при Яд= 1,076 у=1,25 и Р(Г)=0,94. Эти данные свидетельствуют о том, нто надежность дефектного трубопровода резко снижается по сравнению с бездефектным. Толщины стенки, определенные выше для бездефектной трубы, оказываются недостаточ-