
 |
|
|
Главная Переработка нефти и газа т ----- Подставляя эти зависимости в уравнение (7.2-38), получим После подстановки полученного значения v в уравнение (7.2-37) будем иметь dh=-;[f е-"Ре-"(---р) dl. (7.2-39) Пусть Ьл(Т„,,-Пр)=.Б и р-е-РЛ, тогда й,р=( Ле-ве-й/. о Пусть Ве- = и тогда 6-™ = - . Следовательно, /= --1п4 и dl =---du. т В ти После подстановки постоянных в это уравнение получим К,-~=- du. Так как В оо оо J " = J " - j « = Ei (-В) -Ei {-В), и=В и=В и=В имеем Л = Р """" (Г,, ,-Т)]-Ei [-bn (Г,, 1-Г,р) е-*]}. Вводя v„=vie"roci из уравнения (7.2-38) и (Гос i - 7гр)е-« ~ Тос 2 - Ггр, подразумеваемое по уравнению (7.2-15), получим: лгр=Р 1- (Ei[-ft«(r„,,-np)]- -Е![-6«(Г,,2-Г,р)]). (7.2-40) 10 147 Это уравнение можно упростить следующим образом: -=Р-ДА. (7.2-41) В этом случае с учетом уравнения (7.2-37) игр можно интерпретировать как потери напора при изотермическом течении жидкости, вязкость которой в начале трубопровода равна vi; А/ - поправка, учитывающая охлаждение жидкости вдоль участка трубопровода; Лг - радиальная температурная поправка. При ламинарном течении p=128/ng и 6 = 1, а при турбулентном p = 0,201/g и Ь = 0,25 (если коэффициент трения X определен по уравнению 1.1-4). В уравнении (7.2-41) eMoci-rp) А/ =--1- (Ei [-Ьп (Г„, 1-Ггр)) - И 1-Ьп (Г„, 2-Пр)11 и, следовательно, Д( - поправка, учитывающая охлаждение потока в осевом направлении и указывающая, во сколько раз растет потеря напора вследствие того, что температура нефти за время движения потока постепенно понижается с 7ос i до 7ос 2," Аг - поправка, учитывающая охлаждение потока в радиальном направлении. Эта поправка была бы неизменной, если бы температура нефти в любом поперечном сечении трубопровода оставалась постоянной. Однако фактически температура нефти уменьшается от оси трубы к ее стенкам и, следовательно, вязкость нефти у стенок выше, чем на оси трубы. Аг учитывает это. Для определения этой поправки Черникин использовал отношение Сейде-ра - Тейта Аг = г-у, (7.2-42) где Vtp. в и Voc- соответственно средние значения вязкости нефти у стенок трубы и вдоль ее оси, которые определяются на основе средних арифметических значений температур нефти в начале и в конце отрезка трубопровода; ё и со - константы (е равно 0,9 для ламинарного и 1 для турбулентного потоков; ш составляет от /з до u при ламинарном и от 7з до /? при турбулентном потоках). В трубопроводах, по которым транспортируются вязкие нефти, переход от ламинарного к турбулентному течению можно ожидать при числе Рейнольдса, равном примерно 2000. Уравнение (7.2-41), пригодное для проведения сравнительно быстрых расчетов, ограничивается в следующих случаях: 1) если коэффициент теплопередачи К остается постоянным вдоль всего трубЬпровода, хотя фактически он может существенно измениться, особенно при неизолированных трубопроводах; 2) если для определения коэффициента трения при турбулентном потоке применено уравнение Блазиуса, которое действительно для гладких труб; точность расчета увеличивается при введении постоянных а и Ь -см. уравнение (7.1-4); 3) уравнение (7.2-38) выражает приближенную зависимость вязкости от температуры, которая действительна для крайне ограниченных значений температуры; 4) постоянные е и со колеблются в достаточно широких пределах и, следовательно, Аг не может быть определено с желаемой степенью точности. б) Теория Форда (модифицированная) Определение потерь напора в потоке нефти по этой теории основано на применении метода конечных разностей, это позволяет учитывать изменения К и использовать точные значения коэффициента трения и вязкости (Форд, 1955). Ниже описан этот метод в несколько видоизмененной форме. Исходя из того, что начальная температура нефти по оси трубы равна 7"ос ь полагаем, что температура нефти АГос будет понижаться незначительно на относительно коротком участке трубы 1\. Это означает, что средняя температура на длине этого участка трубы с достаточной степенью приближения составит Тос 1 = 7001-0,5ЛТ„,. (7.2-43) По уравнениям (7.2-15), (7.2-17) и (7.2-30) можно рассчитать длину 1\ участка трубы, на которой падение осевой температуры равно А7ос. Для выполнения расчета необходимо определить коэффициент теплопередачи, как это указано в примере 7.2-3, а затем среднюю температуру стенок трубы Гтр. в. После этого находят взаимосвязанные значения параметров Точ, Т.т, 7"из и /, что позволяет построить кривую зависимости температуры от длины трубы. Значение вязкости, соответствующей числу Рейнольдса Re = 2000, которое характеризует момент перехода ламинарного потока в турбулентный, определяется по уравнению (7.1-2); для определения температуры Тос, соответствующей критической вязкости нефти, необходимо построить график зависимости Т - v. Точка на графике, соответствующая этой температуре, будет указывать на область перехода турбулентного течения в ламинарное. При расчете потерь напора в турбулентном потоке температура трубопровода может быть приравнена /ОБг-Рг к 7-ос. Однако при ламинарном потоке р„, 7.2.11. График для определения температурная разница нефти по оси откорректированной температуры Г„ трубы и на ее стенках настолько зна- (Форд 1956) чительно различается, что необходимо . , определять в каждом случае среднюю температуру. Из практики известно, что среднюю температуру потока проще всего определять с-помощью графика, построенного по опытным данным (рис, 7i2.-ll). Отю-мощью этого графика можно определить изменения откорректирован* ной температуры Тн вдоль трубопровода; 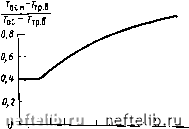 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 [ 45 ] 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 |
||
 |
 |