Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 [ 66 ] 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84

соответствующими направлению вращения. Абсолютное значение скорректированной величины пропускной опособности для отвода 2, вычисленное по уравнению (8.3-21), не приведенное в таблице, равно 5,304X10" мс. Расход газа в отводе 14 приравнивается этому значению и затем корректируется, используя коррекцию для участка D и уравнение (8.3-21). Полученное значение равно 4,076X10-2 м/с, и соответственно пропускная способность отвода 2-4,076X10 м/с. Эти значения заносят в колон-Таблица

ку 10. Итерация продолжается с qi колонки 10. Повторяя вычисление семь раз, получают значение последнего расчета. Окончательные результаты сводят в колон-

ках 11-,14. В каждом случае

2 Ар.

находится в пределах 5 Па (колонки 12).

В колонках 13 и 14 даны величины pi г и рт давлений соответственно в начале и конце отводов, основанные на данных падения давления, приведенных в колонке 12, и условия pii=3300 Па в узловой точке с отводами 1 и 4.

Основным преимуществом метода Кросса является его простота, а недостатком - медленная сходимость, которая делает этот метод неэкономичным. Для устранения этого недостатка Ренауар усовершенствовал вариант метода Кросса (1968 г.). Метод Ренауара приемлем для моделирования установившихся потоков в несложных кольцевых газопроводных сетях. Методика Ренауара была обобщена Пернеллем и использовалась для расчета газовых сетей любого размера (1968 г.). Сущность последнего метода состоит в следующем. В предыдущем примере была необходима коррекция пропускной способности для каждого кольцевого участка в каждом этапе итерации. Отметим, что коррекция, должна рассчитываться путем Aqa для участка А, Адв - для участка Б и т. д. Коррекция пропускной способности отвода (отводов)

общих для участков А и В определяется как (Адл-Адв), общих для участков В и С - как (Дв-Aqc) и т. д.

Уравнение (8.3-20) позволяет нам дописать для п кольцевых участков л линейных уравнений в п коррекциях пропускной способности А<7а, AQb. Aqc и т. д. Коррекции определяются решением этой системы

а.3-3

уравнений. После коррекции полученные значения проверяются, чтобы видеть, соответствуют ли они (8.3-13); если совокупность падений давления кольцевых участков превышает заданные пределы, то процедура повторяется. Этот метод обеспечивает достаточно точный результат в два или три этапа, даже если первые оценки дают широкий разброс.

Метод Стонера для расчета кольцевых газопроводных сетей основан на уравнении неразрывности (Стонер, 1970 г.). Этот метод имеет преимущество; если метод Кросса используется только Для составления карт пропускных способностей и давлений сетей, то метод Стонера дает любые параметры (диаметр трубы, отвода, мощность компрессора, число скважин в подземном хранилище, диаметр штуцеров для снижения давления в газопроводах и т. д.) комплексных систем. Однако этот метод очень сложен и требует значительно большего времени ра боты вычислительных машин.

Схема для расчета этим методом приведена на рис. 8.3-7. Узловая точка 11 выбрана как пример. Газ по газопроводу подают на прием компрессора 13 и потребителю. В точке 11 в газопровод поступает газ

,4- 2П

из подземного хранилища 12. Уравнение неразрывности для точки 11 запишется в виде

i--(7i2-ii)x-(?i3-ii)k + (?io-ii)tp-<7вых11=0, (8.3-25)

где индексы X - газовое хранение, к - компрессор, тр - трубопровод, вых - отбор газа из точки 11.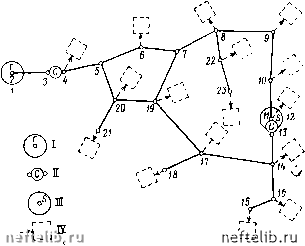

Рис. 8.3-7. Региональная газопроводная система;

/ - газовое месторождение; - компрессорная станция; / - газохранилище; /V - потребитель

Поток газа в узловую точку положителен. Fn равно нулю, если узловая точка сбалансирована, то есть если удовлетворяется условие fj<e, где Ё -допустимая погрешность. Вводя в это уравнение зависимости (8.3-1), (8.3-7) и (8.3-11), мы получим

F11-•12-11 (Pi2 ~Pii 1)/1-Sia-ii"

Pl3-ll

+

,, .0,5 10-11 Чяых 11 - J,

«i) 10-11

(8.3-26)

где Si.j - коэффициент знака, зависящий от направления потока газа.

s,,,=3„»(p.-p,)=

I - 1, если Рг < pj.

Записав п уравнений непрерывности для п узловых точек системы, мы получим нелинейную систему уравнений, представляющую математическую модель системы при установившемся режиме течения газа. Уравнения содержат {2п.-\-т) параметров, где п - количество узловых точек, а т - число участков газопровода, входящих в узловую точку. Мо-