Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 [ 43 ] 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139

A(t) dAl

Рнс. 4.10. Схемалнсское првдспвлшиершшроетраншня зоны, эшштой шро» в моделв Мцжса н Лангенхейма:

1 - модель; 2 - теплоноситель; 3 - зона с повышенной темпфатурой; 4 - зона с низкой температурой

ИЛИ же снижают скорость распространшия зоны постоянной температуры, возникающей при нагнетании теплоносителя, в котором происходят фазовые переходы (например, конденсируницегося водяного пара).

Для пол}ения первого представления о масштабах тепловых потерь 0&1ЧН0 рассматривают горизонтальный слой постоянной толщины Н. Процессы внутри слоя можно изучать двумя способами: аналитически или решением уравнений численными методами.

Для быстрого определения порядка величины потерь теплоты удобнее пользоваться аналитическими методами. Именно зти методы будут рассмотрены ниже. Все математические выводы будут рассмотрены применительно к одномерному течению жидкостей и однородным твердым телам. Для этого необходимо сделать ряд упрощающих допущений, а именно: допущение постоянства Ф, р, с, X каждой из рассматриваемых сред. Дальнейшие допущения различны в различных моделях и зависят от вида нагнетаемого теплоносителя (нагретой воды или пара).

Нагнетание насыщенного водяного пара. Даже если принимать во внимание изменоше температуры конденсации водяного пара в ходе его продвижения, профили температуры имеют особую точку на фронте кондгасации, в которой резко меняется характер температурного профиля. Это было использовано Марксом и Лангенхеймом [4.12], которые предположили, что в проницаемом слое зона повышенной температуры продвигается, как поршень (рис. 4.10). При этом были сделаны следующие допущения:

потеря напора, вызванная протеканием теплоносителя, столь мала, что зона, занятая паром, может считаться изотермической с температурой, которая равна температуре Т* теплоносителя, нагнетаемого в пласт;

тешкшроводность в продольном направлении и теппоперенос вследствие конвекции вне зоны, занятой паром, малы, следовательно, темпе-

ратура на границах этой зоны постоянна и равна началыюй температуре нефтеносного пласта;

теплшроводность пласта в вертикальном направлении бесконечно велика, так что зона повышенной температуры ограничена цилиндрической поверхностью.

В данной модели учитывается только вертикальная составляющая dTldz температурного градиента в окружакхцих породах и не рассматривается составлякяцая, параллельная пласту, а также геотермический гра-дигат в породах.

Вначале следует найти зависимость величины утечек тепла q(f) через окружающую породу от расширения нагретой зоны Дг).

Пусть в момент времени г граница нагретой зоны достигнет точки М. Допустим, что начало оси координат z лежит на плоскости, делящей толщину нефтеносного слоя пополам. Если следовать сделанным допущениям, температурный профиль в нефтешоюм слое, рассматриваемый вдоль вертикали, проходящей через точку М, должен удовлетворять следующим условиям:

<<т T(z.t)=T, (4.56)

где ар - коэффицигат температуропроводности окружакяцего грунта (ар = \р1 (рс) р,Хри (р cfp считаются постоянными величинами.

Решением (4.56) является локальная температура 7Xz, t) окружающей породы: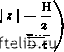

ту -т, vr

функция (4.57)

называется дополнительным интегралом вероятностей.

Тепловые утечки dq в окружающую породу в единицу времени и увеличоше поверхности зоны dA, занятой паром, за время г можно записать так:

dg (I. --d = dllJAll lA d-

\dzj ,= ±ni2 ViW= dr (4.58)

в о&цем случае, когда теплофиэические свойства грунта различны и равны HVjL с одной стороны пласта, и ар2 и \р2 - с другой, тепловые потериq [A(t)] через поверхность A(t) равны

. -- dr .

(4.59)

Для оценки интеграла необходимо знать закон распространения зоны, заняп пм. Количество теплоты Q(f), переносиьюе поступашцим в пласт тешкхюсителем, определяется разностью энтальпий ТС* пароводяной смеси, нагнетаемой в пласт, и 3 воды при температуре месторождения (см. раздел 3.1):

(t) = т - SfGr) = .и [с. (т* - т,) + Х**] ,

(4.60)

где m - массовый расход нагнетаемого теплшосителя; - удельная теплоемкость воды в температурном интервале от 7у*до L* - скрытая теплота парообразования воды, температура которой равна rj X* - сухость пара в пводяной смеси, нагнетаемой в пласт.

Бели {рс)* - коество теплоты в единице объема зоны повышенной температуры -(обьеьгаая теплоемкость), то тепловой баланс системы зашюывается в следуннцем виде:

Ог<; =(pc)*(t*-.t,)h---f [

Используя уравноше (4.59), получаем интегрально-дифференциальное ураивение, аналитическое решение которого возможно при Q = const.

С использованием преобразования Лапласа это решоше имеет следующий вцд:

s*(pc)* (т*-т,)

2 8V1

v-a н

ygFi

{рс)*1{рс)п (рс)*/(рс)

(4.62) (4.63)

Объемную теплоемкость *, которую считиот постоянной, можно найтн. если учесть средние значения насьццения sjc для теплоносителей, находящихся в нагретой зоне, т.е.

№здекс s относитсн к коллектору нефтеносного слоя.