Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 [ 22 ] 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78

ГЛАВА V.

ТЕМПЕРАТУРНОЕ ПОЛЕ УПРУГОГО ПЛАСТА

§ 1. ПОСТАНОВКА ЗАДАЧИ итоге исследований тепловых

процессов, сопутствующих движению несжимаемых жидкостей в пористой среде, обнаружено, что в случае непостоянной скорости фильтрации взаимосвязь между температурой и давлением усложняется и практические возможности использования температурных кривых для зондирования гидродинамического состояния пласта значительно снижаются.

В реальных пластовых системах невозможно сразу же после пуска скважины создать установившийся ноток жидкости во всем объеме пласта. В случае постоянной депрессии на забое приток жидкости к скважине во времени затухает, а скорость фильтрации на заданном расстоянии от оси скважины вначале возрастает, а затем надает. При постоянном отборе жидкости уменьшается забойное давление, а скорость фильтрации с ростом расстояния от оси скважины неизбежно снижается. И в том и в другом случае пластовое давление падает со временем, в результате чего в уравнении энергии появляется член, содержащий частную производную давления но времени. Пока значение этого члена не изучено, трудно предвидеть эффективность температурных исследований в реальных промысловых условиях. Поэтому изучение дроссельного движения упругой жидкости представ.ляет определенный практический интерес.

В основу наших исследований положим систему уравнений, слагаемую из уравнения сохранения энергии в потоке упругой жидкости (III. 51) без учета теплопроводности

-Ь U [grad Г -Ь 8 grad г,, Я - = О, (V. 1)

где П ~ ту - (другиеобозначения как в формуле (III. 51)), и урав-

нения сохранения массы жидкости, которое с учетом законов Дарси и Гука приводится к виду

X div grad р = -2-. (V.2)

Здесь к - коэффициент пьезопроводности пласта. 72

Принимаем, что пьезопроводность практически не зависит от температуры в пределах небольших колебаний, вызванных, например, эффектом Джоуля-Томсона. Таким образом, предполагают, что изменения температуры суш;ественно не влияют на распределение давлений в пористой среде; значит уравнение (V. 2) можно решать независимо от (V. 1), а затем использовать полученное решение гидродинамической задачи для подстановки в уравнение (V. 1), чтобы определить температурное поле.

Кроме прямого решения системы дифференциальных уравнений, в настоящей главе предлагается метод приближенного определения температурного поля пласта в условиях неустановившейся фильтрации.

§ 2. МЕТОД ПРИБЛИЖЕННОГО Уравнение энергии ш-устано-ОПРЕДЕЛЕНИЯ вившегося потока упругой жидко-

ТЕМПЕРАТУРНОГО ПОЛЯ сти (V. 1) представляет собой ли-НЕСТАЦИОНАРНЫХ ПОТОКОВ нейное неоднородное дифференциальное уравнение первого порядка S частных производных с переменными коэффициентами. Интегрирование такого уравнения для общего случая связано с известными затруднениями. Предлагаемый ниже приближенный метод определения температур в нестационарном потоке не претендует на высокую точность, но отличается простотой и может найти практическое применение. В основу метода положены физические закономерности, изученные при исследовании стационарных задач.

Наблюдая за точкой, передвигающейся в пористой среде по течению со скоростью конвективного переноса тепла, замечаем, что температура в этой точке может измениться как за счет дроссельного, так и адиабатического эффектов. Запишем полный дифференциал температуры по пути движения

dT = -sMdl + r]ndt, (V.3)

где 8 - коэффициент Джоуля-Томсона; т) - температурный коэффициент адиабатического расширения; I - путь; t - время; П =

fJlCw

- --; т - пористость; c„ и Сп - теплоемкости жидкости и нори-стой среды.

Корректность дифференциала (V. 3) несомненна, так как частные производные температуры, соответствующие этому дифференциалу дТ до дТ гг др

- = - Sj- И -д= г]П, удовлетворяют уравнению энергии

потока сжимаемой жидкости (V. 1). Представим уравнение (V. 3) так

Здесь а = . (V. 4а)

Первая сумма (в скобках) является полным дифференциалом давления, следовательно.

dT = -Sj [dp-{i+a)

(V. 5)

Физический смысл выражения (V. 5) объясняется графически на рис. 14. В наблюдаемой точке О, которая перемещается со скоростью конвективного переноса, давление падает за время At = t - t по кривой ОК. Точка О лежит на кривой распределения давлений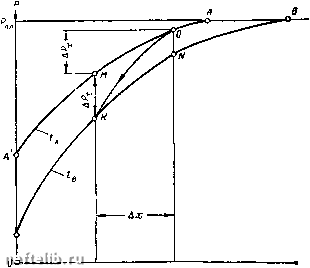

Рис. 14. Кривые распределения давлений в моменты времени tj и tg.

АА, отвечающей моменту времени t

точка К - на кривой ВВ, отвечающей моменту t. Изменение температуры в наблюдаемой точке соответствует согласно (V. 3) понижению давления Ар (х) по пути ОМ и изменению давления Ар (t) во времени в результате перераспределения давления МК. При достаточно малых интервалах пути Аг и времени At значение Ар (ж) по пути ОМ и МК так же как и расстояния ON и МК, отвечающие значению Ар {t), будут равны до второго порядка малости. Тогда будет справедливо соотно шение (V. 5); дифференциал давления dp будет отвечать фактическому изменению давления по линии ОК. Для случая монотонно изменяющегося давления в пористой среде по пути и по времени действительное значение температурных отклонений заключается в пределах

[Ро -Рм)- (Рм - Рн)

{Pn-Pk)-(Po-Pn)];

(V. 6)