Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 [ 48 ] 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78

Сумма указанных выше изменений теплосодержания приводит ж изменению температуры в элементе объема пористой среды, что дает искомое уравнение

Я div grad Г - Спи grad Г + ш = Сп. (IX. 4)

Уравнение температурного поля с источником тепла (IX. 4) отличается от обычного уравнения (VII. 51) наличием дополнительного члена W, учитывающего удельную мощность источника тепла. Значение w уточняется в теории горения: оно зависит в основном ют температуры Т, которую нужно определить, поэтому конкретное решение полного уравнения (IX. 4) без упрощений и схематизации можно получить только с помощью быстродействующих вычислительных приспособлений.

Для радиального случая уравнение (IX. 4) перепишем так

W дТ

•Go - расход теплоносителя.

В зоне горения изменяется произведение Ср Gq (мощность тепло-конвекции) и поэтому параметр К становится переменным» что еще •больше усложняет решение задачи. Тем не менее, основные закономерности и характер передвижного очага горения в пористой среде может быть выяснен с помощью аналитических решений уравнения «(IX. 5) после некоторой схематизации фзпякций К т w. Для этого «знакомимся с основными положениями теории горения и результатами экспериментов по созданию очага горения в пористой среде.

Лабораторные опыты зажигания нефтей в песках и песчаниках [56] показали, что в процессе предварительного нагревания насыщенной нефтью пористой среды легкая нефть уносится потоком воздуха или кислорода. В момент достижения температуры воспламенения в пористой среде остаются лишь продукты разложения остаточной нефти в виде кокса. Легкие нефти почти не оставляют кокса в нагретой зоне и поэтому они не зажигаются в пласте. Для зажигания в пласте пригодны лишь некоторые сорта очень тяжелых и смолистых нефтей.

В нагретой пористой среде, лишенной остатков горючего, можно создать очаг горения путем нагнетания газовоздушной смеси [81 ]. В этом случае внутри пористой среды образуется регулируемый извне передвижной очаг горения, являющийся весьма перспективным средством для реализации тепловой обработки пласта. Не случайно этому вопросу уделяют в последнее время очень много внимания за рубежом [57].

§ 2. из ТЕОРИИ ГОРЕНИЯ Процесс горения как всякая»

ГАЗОВОГО ТОПЛИВА химическая реакция подчиняется

закону действующих масс. Скоростью реакции называют скорость образования одного из продуктов горения, или (что одно и то же) скорость расходования какого-либо исходного вещества.

Согласно закону действующих масс скорость реакции газовых; веществ при постоянной температуре выражается уравнением

wi = к,р1р%, (IX. 7)

где р - текущее парциальное давление; А ж В - индексы исходных реагирующих веществ; аир - показатели степени, соответствующие числу молей участвующих в реакции исходных веществ; ki - постоянная скорости прямой реакции.

Скорость обратной реакции выражается так

ц; = fepvp*,, (IX. 8>

где С VL D - индексы продуктов реакции; Y и б - числа их молей;. 2 - константа скорости обратной реакции.

Из условия термодинамического равновесия прямой и обратной реакций или для случая Wy = получаем из (IX. 7) и (IX. 8) математическое выражение для константы равновесия кр при постоянной температуре

Например, для реакции 2H2 -Ь O2 2Н2О получим: кр =

РН-20

Строго говоря, область применения закона действующих массг (IX. 9) ограничивается идеальными газами. Тем не менее вытекающие из него выводы отражают достаточно верно п равновесие реальных реакций в газовом состоянии.

По величине константы равновесия кр можно определить состояние равновесной системы при заданной температуре. Зависимость константы равновесия от температуры для реакций, протекающих при р = const, выражается уравнением

кркде (IX. 10)

где ко - постоянное число; Qp - тепловой эффект реакции в ккал/кг; R - газовая постоянная; остальные обозначения известны.

Более полному протеканию экзотермических реакций Qp 0 благоприятствуют низкие температуры, а протеканию эндотермических реакций Qp<i О - высокие температуры.

Зависимости (IX. 9) и (IX. 10) определяют лишь состояние уже наступивших химических равновесий при изменении температуры и давления, а не влияние температур и давлений на скорость реакции.

Скорость реакции определяется законом Аррениуса эмпирического происхождения, который в экспоненциальной форме выражается так

(IX. И)

тде Е и Wo ~ эмпирические коэффициенты, причем коэффициент Wo зависит от давления.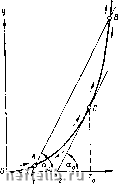

г о

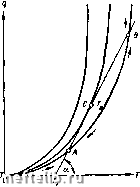Рис. 27. Кривые скорости реакции горения в зависимости от температуры Т

и давления р.

Итак, скорость реакции в газовой среде зависит от температуры И давления реагирующих веществ. При комнатной температуре реакция в горючей смеси протекает очень медленно; поэтому можно -считать, что смесь не реагирует, и ее температура равна температуре окружающей среды. По мере нагревания смеси увеличивается скорость реакции и при некоторой температуре уже становится заметной. Благодаря увеличивающемуся выделению тепла горючая смесь нагревается. Разность температур между смесью и окружающей средой обусловливается тепловыми потерями, которые увеличиваются с ростом температуры. Равновесие наступает, когда все выделившееся из реагирующей смеси тепло отводится в окружающую среду. При недостаточном отводе тепла происходит прогрессивный разогрев смеси, приводящий к самовоспламенению или взрыву.

Зависимость теплового выделения и тепловых потерь от температуры изображена на рис. 21,а. Интенсивность теплового выделения q выражается экспоненциальной кривой ОАСВ, поскольку скорость изменяется в соответствии с законом Аррениуса.