Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 [ 46 ] 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78

Для таких ограниченных участков ствола скважины получаем из (VIII. 46) известную трубопроводную формулу

р-Рп = 2срйГер--АЛ, (VIII. 48)

где ро и Рп - давления на границах рассматриваемого участка ствола скважины; Гер - усредненная температура на данном участке трубы.

Для дальнейшего упрощения задачи необходимо уменьшить наблюдаемые участки ствола скважины так, чтобы было допустимо осреднение параболы прямыми отрезками

Ар = Р„-Рк = 4-. (VIII.49)

Погрешность такого осреднения

II = ± Vmax-Ymm Рн-Рк . (VIII. 50)

2уср Рн+Рк

Оказывается, что при высоких пластовых давлениях большие участки параболы распределения давлений можно заменить прямыми линиями.

Так, для рпл = 250 кГ/см и Я = ± 1 % получаем Ар == 5 кГ/см. Перепад давлений 5 кГ/см в условиях высоких давлений и при нормальной эксплуатации скважины соответствует нескольким сотням метров, т. е. в большинстве случаев почти всему продуктивному интервалу скважины.

Итак, в первом приближении будем принимать

ИЖ -- i = const. (VIII. 51)

dh Yep -О 2gF

Для сохранения зависимости (VIII. 51) и при режиме непостоянного забойного давления необходимо, чтобы изменения давления, происходящие в интервале времени практической стабилизации давлений, были незначительны. Тогда в пределах наблюдаемого участка ствола скважины запишется зависимость

1 I Gl

Ар (Л, t) = p3{t)~--h, (VIII. 52)

где Рз (О ~ забойное давление.

Анализируя уравнения энергии для потока несжимаемой жидкости, мы убедились в том, что точное решение задачи можно получить только для независимого от времени закона теплопередачи (VIII. 6). В случае неустановившейся теплопередачи, определяемой формулой (VIII. 2), рассматривая задачу как: квазистационарную,

можно получить приближенное решение (VIII. 39) для очень медленных изменений значения К (t). На этом основании для газового потока ограничимся решением стационарной задачи, когда уравнение энергии (VIII. 40) с учетом условий (VIII. 10) и (VIII. 51), а также закона (VIII. 6) переходит в следующее уравнение с постоянными коэффициентами

дТ , F Yep дТ 2я ГрО у, F уср

Sep к

Go 2я Го а

Yep D 2gF CpGo

т-А.

(VIII. 53)

Используя преобразование Лапласа по независимой переменной t, переводим уравнение (VIII. 53) в обыкновенное для изображения функции Ta{h, s)

Т (h, s) -I- sNTu (h, s) + NTh 4- Z == 0,

--

(VIII. 54) (VIII. 55)

L = ±-

ё-2г-«о-Лср«Арзи(.) + -

(VIII. 56)

где А77зи (s) - изображение функции изменения забойного давления после пуска скважины.

Общее решение для изображения, как и в случае (VIII. 15), б5дет следующим

(VIII. 57)

т II. „\ Fh L

s sN sN

где постоянная с находится из начального условия Та (О, h) =

= jL + AT,a{s) для ft = 0

С=4- + А7зи(5)+ *

(VIII. 58)

s ---- sN

Итак, получаем решение задачи для изображения искомой функции температуры в стволе скважины

еср к

Ta(h,s)=+y-

2я Гр а

2п гра

OpGo

2л го а h

1 е "р-о ] + АГзи(8)е "Ро е

(VIII. 59)

Обратное преобразование функции (VIII. 50) дано формулами (VIII. 20) и (VIII. 21) за исключением члена, содержащего

изображение заданной функции забойного давления АРд (t), оригинал которого получается в виде свертки

s-\--

opYcp

г* -

•Tlcp

е VpVcp сгДрз(т). (VIII. 60)

Таким образом, решение задачи для оригинала функции температуры в стационарной области z<wt представляется так

T{h, t)=T,-rh+{Mr-\-r)

2яг„а

2я rp g . 2a , л 2a --- h--( +-1

+ Tlcp e cP I e ""o cp "p dpa (t).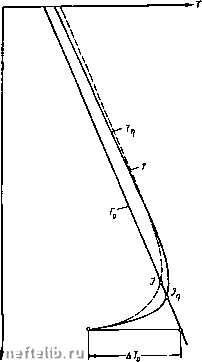

(VIII. 61)

- Yep 2gF

(VIII. 62)

Решение (VIII. 61) для восходящего потока газа в скважине отличается от решения (VIII. 24) для потока жидкости значением постоянного члена и дополнительным членом, учитывающим эффект адиабатического охлаждения газа при постоянном давлении.

Физический смысл первых четырех членов решения (VIII. 61) изучен на примере потока несжимаемой жидкости (VIII. 24- VIII. 26). Новым является последний член решения (VIII. 61). На забое (А = 0) последний член дает нулевой эффект, так как забойная температура опреде-л ляется температурным режимом

Рис. 25. Температурные кривые по пласта, т. е. функцией Tg{t). По стволу газовой скважины. мере удаления от забоя расширя-