Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 [ 44 ] 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78

На некоторой глубине ha производная температуры меняет

знак. Точку на глубине называют точкой инверсий температуры.

Значение найдем по (VHI. 27) из условий ~ = О, а именно

Как видно, глубины (VHI. 28) и (VIH. 29) совпадают лишь в случае, когда М - - ""Т/ - 1 = О, т. е. при отсутствии ги-

дравлических потерь в стволе скважины. Обычно при нагнетании жидкости в скважину < 1 > поэтому М <С. i, а следова-

тельно, йи< Лц.

Так, при нагнетании воды = 1 ккал/кг °С в количестве = = 120 т/сутки = 5000 кг/ч, нагретой до температуры 100° С или АГц = 80° С, в скважину радиусом = 0,1 в случае геотермического градиента Г = 0,03 град/м, М = 0,003 град/м и а = = 4 ккал/м • ч-°С получаем по формулам {VIII. 28) и (VIII. 29) hg 2800 м; К = 1600 м.

Таким образом, нагнетание горячей воды в глубокие скважины для нагревания пласта очень мало эффективно.

При нагнетании холодной воды точка инверсии отсутствует (см. рис. 23), поэтому холодная вода в какой-то мере охлаждает пласт дополнительно.

Для точных законов теплопередачи, учитывающих геометрию теплопроводного потока и теплопроводность горных пород, как, например, (VIII. 2), (VIII. 3) и т. д., оригинал изображения (VIII. 18) оказывается чрезвычайно сложным. Покажем это на примере плоскопараллельного потока. Подставим в (VIII. 14) изображение функции (VIII. 3)

~ (VIII. 30)

у nat у as

и получим

N = - + -(VIII.31)

Оригинал второго члена решения (VIII. 18) можно найти в книге А. В. Лыкова [37]

/± 1 eerfc6l/< , (VIII. 32)

(M + r)w , (М + Г) W s/s{/7+b)

где b = ~-- ; 6 - ширина щели.

Как видно, функция (VIII. 32) не зависит от аргумента и аналогична функции (VIII. 20), определяющей изображение геотермической температуры на расстоянии z "wt. Для очень больших

глубин источника питания и больших интервалов времени произведение е erfc b У t О и тогда нарастание температуры выходящего потока подчиняется формуле

(Vin.33)

в отличие от решения (VIII. 25) для закона теплопередачи Ньютона решение (VIII. 32) при неограниченной глубине потока не дает ограниченного предела приращения температуры выходящей из глубины жидкости.

Оригинал изображения, зависимого от ординаты z, имеет следующий вид

{М + Г) we

-kVs

s/s{y s + b) ~{l + bk) erfc

(M + r)w

/! i;4-)

\ in

X erf«

Здесь

KLz

CpGo y a

(VIII. 34)

(VIII. 35)

Очевидно, что для z wt значение (VIII. 34) равно нулю и действует закон (VIII. 32). Для малых значений аргумента z и больших значений времени ( решение (VIII. 34) упрощается

Уа--

-khz

(VIII. 36)

CpGo у а .

Разность между значениями (VIII. 34) и (VIII. 36) в соответствии с (VIII. 18) для > Z дает предельное приращение температуры восходящего потока

АГшах = (ЖЧ- Г) Z.

(VIII. 37)

Это значит, что предельная температура в потоке в вертикальной щели Т (z, г) = Гц -Ь М Z не зависит от геотермического градиента и при М (=« О она близка к температуре глубинного источника T{z)

Оригинал функции (VIII. 18) для радиального закона теплообмена (VIII. 2), представляющий точное решение температурной задачи для вертикального потока несжимаемой жидкости в трубах, еще не найден. Учитывая актуальность этой задачи, попытаемся обосновать применимое для практических целей приближенное решение, которое получается после замены функции (VIII. 2) ступенчатой функцией.

Благодаря быстрому распространению температурных сигналов но стволу скважины и, в связи с этим, быстрой стабилизации температур в потоке при постоянном значении коэффициента теилоиередачи а можно утверждать, что скачкообразным изменениям коэффициента а, происходящим через достаточно длительные интер-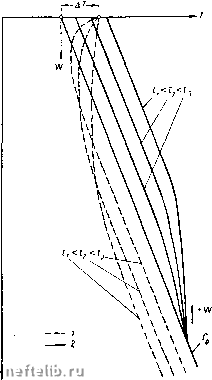

валы времени А<>-

будут

соответствовать стационарные распределения температур в стволе скважины на конец каждого периода, определяемые формулой (VIII. 24) для постоянного значения коэффициента а.

Если коэффициент а - очень медленно затухающая функция времени, то эту функцию можно заменить ступенчатой функцией, падающей скачкообразно через интервалы

времени At= . В конце каж-

Рис. 24. Квазистационарные распределения температур в стволе скважины.

1-нагнетательная сквашина; 2-нефтяная сквашина.

дого периода времени Д t кривая распределения температур в скважине становится стационарной. На самом деле значение а {t) меняется непрерывно и в стволе скважины протекает процесс, близкий к квазистационарному. Фактическая же квазистационарная эпюра температур для момента времени t будет находиться в пределах стационарных эпюр (VIII. 24) для моментов времени

t--- ш t -\--. Относительную погрешность определяемой эпюры

W W

температур по ступенчатой функции а можно определить так

П= ±

dT Ja z да dt 2w

(VIII. 38)