Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 [ 19 ] 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70

Alb системе, равная единице. В точках и и на прямой, соединяющей эти точки, содержание компонента Ai в системе равно нулю. В точке А 2 содержание компонента А равно единице, а в точках Ai и и на прямой, соединяющей эти точки, содержание компонента А равно нулю. Те же рассуждения справедливы и для точки Лд и соответственно для точек и 2 и соединяющей их прямой.

Пусть состав трехкомпо-нентной смеси характеризуется точкой В на диаграмме (см. рис. 33). Содержание компонента А j в этой смеси определяется отрезком х, содержание компонента А - отрезком у, а содержание компонента А - отрезком z.

При давлении вся область, лежащая между кривой 1 и прямой а1а2, является областью двухфазного состояния. Остальная часть диаграммы, находящаяся вне этой области, соответствует однофазному состоянию системы.

При давлении />2 >Pi область двухфазного состояния заключена между кривой 2 и линией AiA.

Пусть теперь состав трехкомпонентной системы характеризуется точкой Во, находящейся внутри области двухфазного состояния. Составу жидкой фазы в этой системе будут соответствовать значения долей компонентов Л, 2 и А, равные хо, уо и zo- Пусть давление в системе равно pi, а температура Ti. Область двухфазного состояния находится слева от кривой 1. Компонентный состав газовой фазы характеризуется координатами Xi, Ух, Zj (точка Bi), а компонентному составу жидкой фазы соответствует точка в2 с координатами Х2, у2 и Z2.

Обозначим «1, «2 и Пд весовое или мольное содержание в системе компонентов 1, 2 и 3, и /г - весовой или мольный состав газовой и жидкой фаз. Из условия материального баланса имеем

рС-диаграмма для трехкомпо-нентного вещества

п\ + п1 + п1 = п,; nl = Xjn„; n] = x.i;

(3.15)

a;i + i/i + zi = l;

ni По Пя

n, + ng = n; -xo, -=Уо; - = %

Отсюда, например, получаем

aig + Xin, = «1 или + = Жо,

откуда

п1 Xi~Xq

(3.16)

Используя дальше соотношения (3.15) и (3.16), имеем

Из трехфазной диаграммы рис. 33 видно, что

xi -хр ДрДз

20-22

На основании же подобия треугольников ВВВо и BoBBi получаем

(3.18)

ng В0В2

Таким образом, соотношение жидкой и газовой фаз оказывается равным отношению отрезков прямой, которая соединяет точки Bi и В2, характеризующие составы жидкой и газовой фаз, и проходит через точку Во, характеризующую общий состав системы. Кроме 3.17), можно получить еще два аналогичных соотношения. Из формулы (3.17) вытекает важное следствие. Если оставить неизменными составы газовой и жидкой фаз, т. е. величины х, у, Zj и X2, Уг, z, а изменять только хо, у о, zo, т. е. общий состав смеси в таких пределах, чтобы точка Во находилась в двухфазной области, то это приведет к изменению соотношения жидкой и газовой фаз. Наоборот, €сли из системы отбирать жидкую или газовую фазу, то ее равновесие не изменится, а будет меняться лишь общий состав системы.

§ 4. КАПИЛЛЯРНЫЕ СИЛЫ

Молекулярные силы взаимодействия между различными веществами, насыщающими горные породы, играют важную роль в процессах извлечения нефти и газа из недр. Капиллярные силы представляют собой одну из форм проявления межмолекулярных сил.

Характер молекулярного взаимодействия зависит от природы вещества. При нормальных расстояниях между молекулами вещества (при нормальных давлении и температуре) взаимодействие молекул выражается в притяжении их друг к другу. При сильном сближении молекул возникают силы отталкивания.

Сила взаимодействия молекул Fo сильно зависит от расстояния г между молекулами при малых г.

Функция Fo (г) для простых молекул, имеющих сферическую форму, имеет вид, показанный на рис. 34.

Представим себе две жидкости А w В, настолько диспергированные одна в другой, что их молекулы равномерно распределены в объеме, который занимают эти жидкости.

Пусть молекулы жидкости В сильнее притягиваются к молекулам жидкости А, чем между собой. Тогда любое случайное скопление молекул В (рис. 35) окажется недолговечным - молекулы жидкости А «растащат» молекулы жидкости В. Жидкость В является в данном случае полностью растворимой в жидкости А.

Если же взаимное притяжение молекул жидкости В намного больше притяжения молекул жидкости В к молекулам жидкости А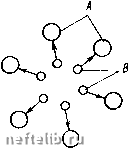

Рис. 34. Зависимость F„ (г)

Рис. 35. Взаимное притяжение молекул А п В

или если между этими разносортными молекулами существуют силы отталкивания, то скопление молекул жидкости В, находящихся в жидкости А, будет устойчивым. Такие жидкости называются взаимно нерастворимыми или несмешивающимися. Следовательно, характер взаимодействия молекул различных веществ определяет их взаимную растворимость.

Рассмотрим схематично молекулы двух взаимно нерастворимых веществ, находящихся в соприкосновении друг с другом (рис. 36).

Будем считать, что молекулы жидкостей А ж В испытывают взаимное отталкивание, причем силы отталкивания действуют в направлении, перпендикулярном поверхности раздела жидкостей. Молекулы А В испытывают также притяжение в сторону той жидкости, которой они принадлежат. Допустим теперь, что молекулы жидкости В, находившиеся первоначально в сильно диспергированном состоянии в жидкости А, собрались в одну каплю. В том случае, когда молекулы жидкости В были сильно диспергированы в жидкости А, они обладали большей потенциальной энергией, чем когда собрались в каплю. Чтобы диспергировать жидкость В в жидкости А, нужно затратить дополнительную работу. Если не