Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 [ 61 ] 62 63 64 65 66 67 68

Допустим, что задача решена. Тогда, зная функции s(i) ис($), можно для каждого вычислить F (s, с), а затем, исключая из указанных зависимостей и с, получить связь между F и s, поэтому каждому 1 отвечает некоторая точка на плоскости s, F в квадрате (0,1) X (0,1), а всему решению - кривая, которую в дальнейшем мы будем называть путем. Поскольку в силу первого уравнения (V.50) = dF/ds, где производная берется вдоль пути (s, F), автомодельное решение однозначно восстанавливается, если он задан. При этом скачкам решения соответствуют прямолинейные участки пути, а угловым точкам - участки постоянства насыщенности; концентрация с на непрерывных участках решения неявно задана соотношением F = F (s, с).

Решающую роль играет то обстоятельство, что путь на (а, F) - диаграмме удается построить, причем зачастую вполне элементарными средствами, до решения задачи. Особенно просто осуществляется построение в случае, если скачок концентрации распространяется без размазывания, т. е. существует подлежащее отысканию значение такое, что

с = с°, 0<i<ic, с = со, ic<i<o3 (V.55)

(достаточные условия распространения скачков концентрации без размазывания указаны ниже).

Используя уравнения (V.50), условия (V.52) и (V.53), и условие устойчивости скачков, можно дать элементарную графическую технику построения пути (s, F) и, следовательно, решения, обобщающую известный способ решения задачи Баклея - Леверетта, изложенный в гл. IV. В построении используются лишь кривые функции F(s, с) при двух значениях: с - начальном и конечном - и значения функций 9 и а, отвечающие этим двум значениям концентрации активной примеси. Это обстоятельство весьма важно, поскольку дополнительно резко ограничивает требуемый объем экспериментов для получения исходных данных к расчетам. Очевидно, решение состоит из (примыкающего ко входу пласта, О < S < S/) участка с с=с°, удаленного участка 5 > в котором концентрация примеси сохраняет первоначальное значение, с = Со, и скачка приS = = S/, на котором изменяются и концентрация, и насыщенность. Первому участку на (s, F) - диаграмме отвечает отрезок кривой F{s, с°), второму - отрезок кривой F(s, Со). Из условий (V.52) следует, что относительная скорость скачка 5/ = mV/U равна угловому коэффициенту отрезка, соединяющего точки s+, F+ и s-, F-, отвечающие значениям переменных по обе стороны скачка (т. е. точно так же, как и в обычной теории Баклея -Леверетта, только соответствующие точки не обязательно располагаются на кривой F{s, с), отвечающей фиксированному значению концентрации примеси). Из условия (V.53) следует, что для скачка, происходящего с изменением концентрации, относительная скорость равна угловому коэффициенту прямой, соединяющей точки s+,F+ или s", р- с «полюсом» -Sp, -Fp,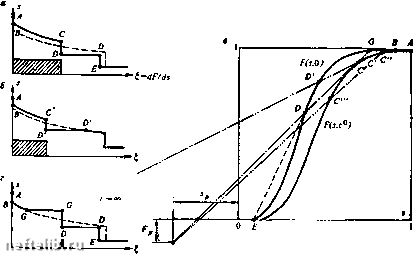

РИС. 59. К решению задачи о вытеснении нефти раствором полезной активной Примеси

Таким образом, точки s+, f+, s-, f- и -Sp, -Fp лежат на одной прямой, и луч, отвечающий скачку, принадлежит пучку, проходящему через полюс (-Sp, -Fp). Чтобы выбрать из этого пучка единственный «нужный» луч, заметим, что им не может быть луч, пересекающий кривую F (s, сР) «сверху» (рис. 59, в), так как при этом вблизи точки пересечения значение автомодельной переменной за скачком больше, чем на самом скачке:

Г = {dF (s, c°)/ds)- > ki = (F- - F+)/{s- - s+), (V.57)

и «решение» получается неоднозначным. Если мы допустим, что луч, соответствующий скачку, пересекает кривую F (s, с") «снизу» (см. рис. 59, в), то в точке сопряжения

I- - (dF/ds)- < S/. (V.58)

При этом число характеристик, приходящих на разрыв, равно лишь двум, и нарушается условие устойчивости скачка (см. подробнее ниже). Таким образом, путь на плоскости (s, F), отвечающий автомодельному решению, обязательно содержит скачок по лучу, проходящему через полюс (-Sp, -Fp) и касающемуся кривой F (s, с°) в точке (s-, с) (см. рис. 59). (Здесь считается, что, как это обычно бывает, такая точка касания единственна. Можно показать, что из нескольких точек касания при построении решения нужно выбрать верхнюю.) После определения положения сопряженного скачка концентрации и насыщенности («с-переход»), дальнейшее достраивание решений в областях двухфазного потока с постоянной концентрацией примеси производится очевидным образом

е е- в л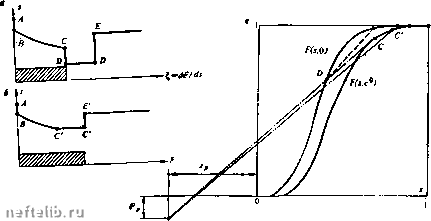

РИС. 60. к анализу процесса довытеснения нефти раствором активной примеси

ПО аналогии с теорией Баклея - Леверетта; два различных варианта возможных путей в (s, F) плоскости показаны на рис. 59.

На рис. 59 показаны соответствующие распределения насыщенностей в один момент времени для вытеснения водой (пунктир) и раствором активной примеси при малой (а) и значительной (б) сорбциях. Во всех случаях фронту примеси предшествует фронт вытеснения нефти водой; если сорбция значительна, он движется с той же скоростью, что и при вытеснении чистой водой. Это означает, что сильно сорбирующаяся примесь не изменяет момента обводнения и начальной стадии водного периода разработки; роль примеси при этом сводится к некоторому замедлению роста обводненности продукции на промежуточной стадии и увеличению полноты вытеснения нефти на заключительной стадии. Если примесь сорбируется слабо (а), то несколько затягивается безводный период эксплуатации и снижается обводненность продукции на начальной стадии обводнения.

Сходное построение позволяет проанализировать и применение активной примеси для довытеснения нефти из залежи, первоначально разработанной при заводнении (т. е. в качестве «третичного» метода). Построение соответствующего (s, F) пути показано на рис. 60, в, а характерные распределения насыщенностей по длине пласта - на рис. 60, а, б. Принципиально возможно образование двух типов решений. Один из них характеризуется отставанием фронта примеси от фронта вытеснения и образованием отчетливо выраженного нефтяного вала. Для решения второго типа характерно образование нефтяного плато с медленным снижением нефте-насыщенности на заднем его фронте; передний фронт плато совпадает с фронтом продвижения активной примеси (см. рис. 60, б). Какой именно из режимов осуществляется, можно определить на (s, F)-диаграмме. Если верхняя точка пересечения касательной к F (s, с°)