Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 [ 66 ] 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217

ttj, моль/м

a,,, моль/м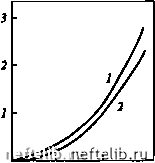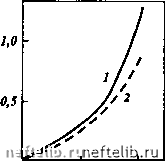

О 10 Сз,моль/м О

а,,,моль/м а;, моль/м-

5 И-С4, моль/м •*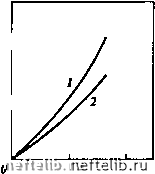

0,5 -

5 (эо-С4, моль/м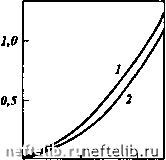

2,5 С 5, моль/м

Рис. 2.78. Изотермы адсорбции компонентов углеводородной смеси: / - в модели пористой среды № 1; 2 - в модели пористой среды № 2

Если П > 1, то ширина переходной зоны определяется, в первую очередь, сорбцией и при ее оценках диффузией можно пренебречь. Если же П < 1, то диффузия играет определяющую роль в формировании фронта вытеснения. Легко видеть, что выражение 2.51 определяет критическое расстояние I, после прохождения фронтом которого диффузия перестает влиять на его формирование. Это критическое расстояние

Z.p = Ai£. (2.52)

Таким образом, на больших расстояниях (L » Lp) ширину фронта можно оценить по выражению

AL, = 2К/,.. (2.53)

Наибольшее значение AL,, как и наибольшее критическое расстояние Lp, имеют наиболее легкие компоненты. Из экспериментальных данных, приведенных в данном разделе, следует, что оценки критического расстояния (2.52) и ширины зоны смеси (2.53) для газоконденсатных систем наиболее целесообразно проводить по компонентам С3 -С. При этом в качестве /С, выбирается некоторое среднее значение, характерное для изотермы сорбции данного компонента.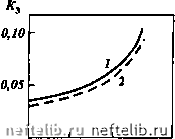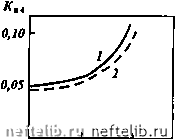

о 10 20 Сз,моль/м О

5 »-С4,м0ль/м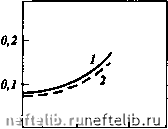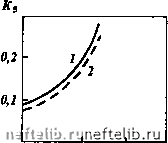

5 1(эо-С4, моль/м о

5 С5,м0ль/м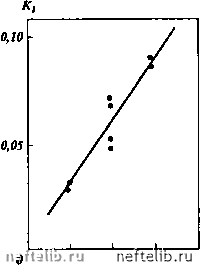

Рис. 2.79. Зависимость коэффициентов адсорбции от молярной концентрации компонентов углеводородной смеси:

/ - в модели пористой среды № 1; 2 - в модели пористой среды № 2

3 4 5 Номер алкана

Рис. 2.80. Зависимость коэффициента адсорбции Генри при низкой концентрации компонентов углеводородной смеси в пористой среде от порядкового номера алканового углеводорода (JC = 0,002, М, = 0,0586).

Верхняя точка каждой пары точек относится к модели пласта № 1, нижняя - к модели пласта № 2, При I = 4 верхняя пара получена для изо-С, нижняя - для H-Cf

Известно, что при отсутствии сорбции ширина зоны смеси пропорциональна L (это видно и из выражения для Лт). В случае сорбируемости примеси при I >> Lp ширина зоны смеси пропорциональна L (см. 2.53). При П = 1 показатель степени при L должен находиться в пределах 0,5 < < л < 1. Действительно, обработка результатов экспериментов для моделей пористых сред № 1 и № 2 (см. табл. 2.20) показала, что л = 0,7. При этом

для модели № 1 (L = 5 м) П = 0,88, для модели № 2 (L = 20 м) П = = 1,76, а Lp = 6,5 м (расчеты проведены по пропану). При аналогичных условиях в пласте критерий будет принимать большие значения, так как характерные расстояния существенно превышают 1р = 6,5 м.

Таким образом, формирование фронта вытеснения в газоконденсато-насыщенных пластах происходит под влиянием двух процессов: диффузии и сорбции. Сорбируемость компонентов пластовой смеси может привести к тому, что фактором, определяющим форму и ширину фронта вытеснения, является сорбция; в этом случае выполняется соотношение П >> 1. В то же время при П - 1 ширина фронта зависит от пройденного расстояния как 1", причем показатель степени л может варьировать в пределах 0,5 < < л < 1, что и подтверждают эксперименты.

Использование формулы (2.53) и данных рис. 2.80 позволяет оценить длины зон смеси как для отдельных компонентов вытесняемой пластовой равновесной газовой фазы, так и для этой фазы в целом. Например, для этана, пропана, бутанов, пентанов длины зон смеси составят соответственно: при пройденном фронтом вытеснения расстоянии 500 м около 1,5, 29,6, 57,6, 85,7 м; при пройденном расстоянии 1000 м около 3,1, 59,2, 115,2, 171,4 м. Для пластовой газовой фазы (по фракции С2+) соответствующие длины зон смеси будут равны 24,4 и 48,7 м, т.е. составят около 5 % расстояния между нагнетательной и добывающей скважинами.

Оценка длины зоны смеси по формуле (2.53) дает наименьшие значения этого параметра, которые следует использовать при определении момента начала контроля за прорывом нагнетаемого газа к добывающим скважинам. Учитывая результаты исследований по испаряемости компонентов С2+ в прокачиваемый газ, а также существенное отличие ожидаемого коэффициента охвата пласта от единицы, при составлении, например, регламента на закачку сухого газа необходимо предусмотреть соответствующие мероприятия контроля на добывающих скважинах в расчетные периоды времени после начала закачки газа.

2.5.4

Математическое описание процесса вытеснения пластовой газоконденсатной смеси сухим газом

Развитие методов численного моделирования и современной электронно-вычислительной техники позволяет эффективно решать реальные задачи многокомпонентной фильтрации.

Математическое описание процессов фильтрации пластовых флюидов сводится к решению краевых задач для системы нелинейных дифференциальных уравнений в частных производных.

Точные или приближенные аналитические решения этих задач, пригодные для практического использования, можно получить для фильтрационных потоков простой геометрии и при использовании различных упрощающих предположений о механизме процесса. Однако большинство реальных фильтрационных потоков имеют сложную форму и описываются системами нелинейных дифференциальных уравнений, получить аналитиче-