Главная  Переработка нефти и газа 

Скачать эту книгу

0 [ 1 ] 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225

Важными оказались решения вопросов взаимодействия потока с взвешенными в нем твердыми частицами (Г. Стоке, Р.И. Шищенко и Б.Д. Бакланов).

Гидродинамика буровых процессов как ветвь науки механики сплошных сред начала формироваться в виде обобщающих работ Р.И. Шищенко, А.Х. Мирзаджанзаде, Н. Мако-вея. Достижения в этой области применительно к теории и практике гидродинамических процессов в бурении были систематизированы в виде учебника для студентов вузов, обучающихся по специальности "бурение нефтяных и газовых скважин", Е.Г. Леоновым и В.М. Исаевым (Е.Г. Леонов, В.И. Исаев. Гидроаэромеханика в бурении. - М.: Недра, 1987).

Сознавая, что авторами упомянутого учебника глубоко проработан материал дисциплины, а изложение его ориентировано в основном на студентов, составители настоящего учебника стремились изложить материал этой главы как можно ближе к изложению аналогичных разделов учебника.

1.1. РАВНОВЕСИЕ И ДВИЖЕНИЕ

ТВЕРДЫХ ЧАСТИЦ

В ЖИДКОСТИ, ГАЗЕ

И ГАЗОЖИДКОСТНОЙ СМЕСИ

Осколки разрушенных горных пород (шлам), поступающие с забоя и стенок скважины, уносятся потоком промывочной жидкости, газа или газожидкостной смеси. Ниже рассмотрены закономерности взаимодействия потока с частицами породы на забое и в заколонном пространстве скважины, необходимые для расчетов подачи насосов при промывке, компрессоров при продувке или тех и других при бурении с использованием аэрированной жидкости.

Витание твердых частиц в потоках жидкости, газа и газожидкостной смеси

Рассмотрим движение твердой частицы со средней скоростью уч в восходящем вертикальном потоке жидкости, текущей со скоростью уп. В общем случае скорости потока и частицы относительно неподвижных стенок

скважины разные. Обычно плотность частиц горных пород больше плотности жидкости, поэтому относительная скорость (рис. 1.1, а)

Уч.(1.1)

имеет ско р ость = 0 называется

v = v - v

Принято, что частица, витая в потоке, vч = 0. Тогда скорость потока в (1.1) при vч скоростью витания vв:

Vп = Vв.(1.2)

Чтоб ы выб р ать среднюю скор ость потока, обеспечивающую транспорт частиц в кольцевом канале на дневную поверхность, нужно уметь определять скорости vв и vч.

Равновесие частицы в восходящем потоке обеспечивается равенством действующих на нее сил, схематично показанных на рис. 1.1, б.

На частицу действует равнодействующая выталкивающей силы и силы тяжести:

R = У(рч - рж)д,(1.3)

где V - объем частицы; рч, рж - плотность соответственно частицы и жидкости; g - ускорение свободного падения.

Сила R уравновешивается силой сопротивления п, которая зависит от реологических свойств жидкости, режима обтекания, концентрации и формы частиц. В дальнейшем будем рассматривать единичную сферическую частицу с эквивалент-

Рис. 1.1. Векторы скоростей (а) и сил {б) для витающей в жидкости твердой частицы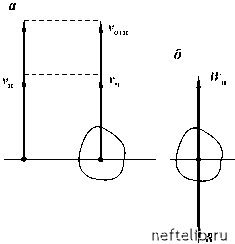

ным диаметром ач = - в неограниченной среде. Экспе-

# п &

риментально установлено, что в этом случае частица при обтекании имеет наименьшее сопротивление. Формула для определения силы сопротивления частицы при обтекании ее вязкой жидкостью, согласно формуле Стокса, имеет вид

= 3пdчVв.(1.4)

Эта формула справедлива для чисел Рейнольдса Re = = VвdчPж/ < 1.

При любых значениях Re силу сопротивления можно выразить в общей форме

= Cw Рж f/ S, (1.5)

где Cw - коэффициент сопротивления; S - площадь наибольшего сечения частицы, перпендикулярного к потоку. Формула (1.5) переходит в (1.4) при

Cw = 24/Re. (1.6)

Приравнивая (1.3) и (1.5) и подставляя V = лdЧ3/6 и S = лdЧ2 / 4, получаем скорость витания для сферической частицы

v = 4 (рч - рж)dч9 (1 7)

В области 1 < Re < 103 следует использовать формулу

Cw = + 0,17Re0665), Re

а для области 10 < Re < 2-105 Ньютон принимал коэффициент Cw = 0,44.

Формулу (1.7) можно записать в виде

v в = K

dч- 1 ,(1.8)

где K = 4д/(3CW) - постоянная Риттингера. Согласно многочисленным данным, при обтекании сферы потоком с Re > 60 примем Cw = 0,4, тогда К = 5,72.

Чтобы выбрать для расчета скорости витания соответст-