Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 [ 5 ] 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225

Течение в трубах

В этом случае (рис. 1.7), так же как и в предыдущем, течение имеет ядро радиуса Е0, движущееся со скоростью w0. Для нахождения перепада давления пренебрегают членами, учитывающими силы инерции и тяжести, и решают систему уравнений в области между стенкой трубы и ядром при следующих граничных условиях:

w = 0 при r = Е = dс/2;

w = w0 = const при 0 < r < Е0;

- = 0 при r = Е 0.

Реологическое уравнение для ВПЖ в трубах при dw < 0

имеет вид

T = -T0 + nw при r > Е0.(1.32)

В результате аналитического решения задачи получают известную формулу Букингама для расхода жидкости, из которой выводят формулу для перепада давления в трубе:

Ар = 2t0L/(EP),

или, вводя значение диаметра dс = 2Е,

Ар = iтL .(1.33)

По формуле (1.33) определяют перепад давления А р (потери на трение) при движении ВПЖ в трубах. Для этого

Рис. 1.7. Эпюры скоростей и напряжений в ламинарном потоке ВПЖ в трубе 18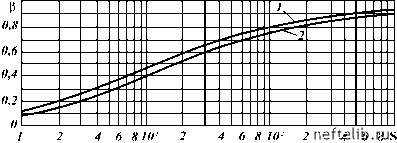

Рис. 1.8. Графики зависимости в = e(S) для круговых (1) и кольцевых (2) каналов

следует вычислить число S, а по его значению определить по кривой 1 (рис. 1.8) величину в и затем по формуле (1.33) найти искомый перепад давления Ар:

x 0dc F

(1.34)

Течение в ольцевом концентричном канале

При течениях ВПЖ в концентричном кольцевом пространстве, так же как и в трубах, образуется ядро, котор ое имеет форму полого цилиндра с площадью поперечного сечения п(Ь2 - а2), боковой поверхностью 2л:(а + b)L и движется со скоростью w0 (рис. 1.9). Это ядро разделяет все течение на два градиентных слоя: /, где производная aw/аг <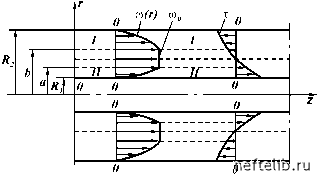

Рис. 1.9. Эпюры скоростей и напряжений кольцевом канале

ламинарном потоке ВПЖ

< 0, и , где производная dw/dr > 0. В связи с этим решают систему уравнений при нахождении профиля скоростей w для каждого слоя отдельно, так как реологическое уравнение имеет свой вид для каждого слоя: для I слоя

T = -T 0 + n-dw ;(1.35)

для II слоя

T = T 0 + n - .(1.36)

Условие равновесия сил, действующих на ядро, записывается следующим образом:

n(fo2 - а2)Ар = 2пт0(а + fo)L.

Граничные условия при отсутствии скольжения по стенкам кольцевого пространства имеют вид:

w = 0 при r = Е1;

w = 0 при r = Е2.

Так как ядро движется с постоянной скоростью w0, то значения распределений скоростей в градиентных слоях на границах с ядром будут w = w0 при а < r < b.

Кроме того, должно выполняться условие

- = 0 при r = a и r = b.

Решая систему дифференциальных уравнений для приведенной модели, получают формулу для определения перепада давления в кольцевом канале:

Ар = 40L ;(1.37)

P(dc - dн)

S = T0(dc - dн)Fк .(1.38)

Коэффициент в (см. рис. 1.8), предварительно вычислив число S, находят по известному расходу, реологическим т0, n и геометрическим dc, dн данным.

Графический метод расчета вручную потерь давления при течении ВПЖ в трубах и кольцевых каналах разработан К.Х. Гродде.