Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 [ 19 ] 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225

Ари = р

dv c

L; ртр = 2-; -v с2рL;

ру - давление в кольцевом канале на устье.

В формуле (1.182) знак плюс при Ар и берется при разгоне колонны, а минус - при торможении.

Гидродинамические давления, возникающие при спуске колонны, когда скважина заполнена вязкопластической жидкостью

Схема рассуждений для определения гидродинамических давлений подобна изложенной выше. При установившемся течении находят потери давления на трение в кольцевом пространстве. Затем вычисляют среднюю скорость vср и инерционную составляющую перепада. Общий перепад получают суммированием двух составляющих перепада давлений.

Чтобы найти перепад давления в кольцевом пространстве при установившемся течении во время спуска колонны, следует решить систему уравнений при следующих граничных условиях:

w = - ит при r = R1;

w = 0 при r = R2.(1.183)

Соответствующий задаче профиль скоростей показан на рис. 1.16. Решение этой задачи относительно расхода q можно представить в виде (Д.А. Голубев):

1 + S2

#1-S

(1 - S)2

l-S#1-S

4 1 - S+ S2

3 (1 - S)2

(1.184)

?Р(1 -S) + ? [?-Р(1 -S)]1n ?-р?(11 -s) + 2[1 - 2Р(1 -S) -- (р (1 -S) + S)2] + р (1 -S-цu = 0.

Т 0R2

(1.185)

Уравнения (1.184) и (1.185) можно представить в безразмерных параметрах

S = 8р /

1 - S2

-S)2 1-S 1

(1 - S)

(1 - S)2

3 # 1 -S 1 + S

S 2 1

1-S2

(1 .1 86)

;в(1 -S) + ? [?-в(1 -S)]ln

-(в(1 -S)+S)2

? - Р(1 - S) 2 + 2в (1 -S)2 ит,

1 - 2в(1 -S) -

(1 .1 87)

где S = TodгFк/(nq); "т = Uтn/(Todг).

При ит = 0 выражения (1.186) и (1.187) преобразуются формулы Фредриксона - Берда, а при т0 0 и ит 0 - решение С.М. Тарга для вязкой жидкости.

Для вычисления параметра S следует находить значение

q = q н + q в = q н + Пит R1 .

(1.188)

При спуске с отключенными насосами (qн = 0) уравнение (1.186) упрощается:

q = q в = пит R1 .

Приравняв (1.184) и (1.189), получают выражения

1 + S2 -

(1 -S)2

S=S2/

4 1 -S + S2

(1 - S)2

2 в (1 -S)2(1 -S2

?(?-в)(1 -S)ln?-в?1 -S) -?S

-?в(1 -S) - J2(1 - 2в(1 -S)) - (в(1 -S) + S)2

(1 .1 89)

(1 .1 90)

(1.191)

S = Todг/(nVcp); = UтS2/(1 в = 4тoL/(dгАp).

S2); S = R1/R2;

(1 .1 92)

В.З. Дигалев привел к безразмерному виду формулы (1 .1 84) и (1.185) при qн = 0 и в результате численных расчетов по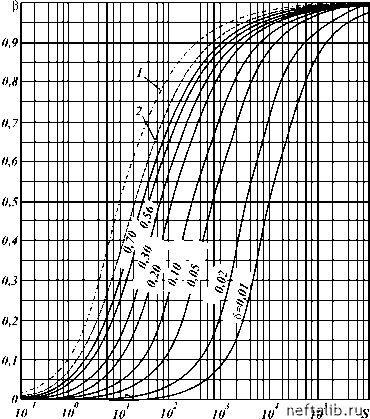

Рис. 1.18. График функции р = р (S, S)

ним построил график р = Р(S, S), который показан на рис. 1.18. На этом же рисунке приведены кривые 1 и 2 с рис. 1.8 при vср = Q/F в каналах с неподвижными стенками.

Схема расчета потерь давления на трение следующая. По формулам (1.192) определяют S, vср и S. Из рис. 1.18 находят р. Перепад давления рассчитывается по формуле

Артр

4т 0L

Формулой (1.192) можно пользоваться при расчетах потерь давлений и при подъеме колонн.