Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 [ 29 ] 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139

Согласно тем же данным, существуют два верхних предела для напряжений сдвига.

Первый соответствует пику кривых, что особенно нагладно при низких давлениях обжима. Его можно считать соответствующим прочности внутренних межконтактных связей в матрице. Второй предел можно считать прочностью насыщенного песчаника, соответствующей пластическому течению матрицы (ее неограниченному деформированию). Те же самые эксперименты [143] показывают, что если применять концепцию эффективных напряжений, то второй предел соответствует линии Кулона (2.163) с углом трения j = 29° и сцеплению « 20 МПа.

Исчезновение "пиковой" прочности при высоких давлениях обжима можно понимать как возникновение пластического течения при незаметном предварительном разрушении контактных связей в матрице.

Ох, МПа ЗООг

200 lOOj-i

= -50 МПа

Г]»-Ш; р. 50

./Г - \--

у/ Рз = -50; р = О (сухая по t-1-1-1 I I I

пористая порода)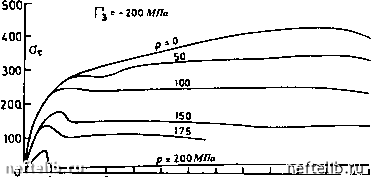

8 10 12 К 16 18 20 22 е .

Рис. 2.5. Зависимости прочности и деформирования песчаника от эффективных напряжений (согласно Дж. Хэндину)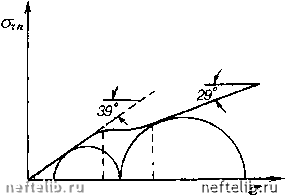

70 100

Рис. 2.6. Зеньшение внутреннего угла трения при дроблении зерен

На рис. 2.6 показан эффект дробления песчинок при давлениях выше 70 атм - согласно [176]. Как можно увидеть, это приводит к излому поверхности текучести (2.167) и соответственно к смене углов трения. Точно такой же эффект наблюдается и в туфах (рис. 2.7), что может быть обусловлено разрушением связей и сменой внутреннего механизма прочности.

Согласно концепции эффективного напряжения для

"1-I-I-г

"1 < i I I I I I г

Пластическое разрушение

-I-I-I-I I I I I .....

о г 3 ♦ J 6 7 в в

Й=---Y- ~ "

Рис. 2.7. Поверхность текучести туфа (данные Р.И. Шока)

вязкоупругой пористой матрицы, насыщенной флюидом, справедлива такая определяющая связь:

а/ = (i: -1 G)e Sy + Ge,j + f Кр Sy +

(2.168)

8xj dxi 3 dxk

где 7j - вязкость при сдвиге и при объемном

деформировании матрицы соответственно.

Этот закон следует применять для расчетов ползучести глин (или горного массива).

2.5.2. ПЛАСТИЧЕСКАЯ ОКРЕСТНОСТЬ СКВАЖИНЫ

Рассмотрим задачу о возникновении пластической зоны вокруг необсаженной скважины, которая может возникнуть при откачке флюидов из массива (задача рассматривалась автором совместно с Т.К. Рамазановым).

Уравнения равновесия, составленные относительно полных напряжений для осесимметричного движения насыщенного массива, имеют вид

1 8 /„ /ч (Jee , d(7 dp „

- - van )-------

r dr r dz dr

(2.169)

r dz r dr dz

где (j/, aef, aи a - соответственно радиальное, кольцевое, осевое и сдвиговое напряжения.

Теперь можно воспользоваться функциями напряжений /