Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 [ 79 ] 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139

5.3. Сейсмика нефтяных и газовых пластов

5.3Л. РЕЛАКСАЦИЯ ВОЛН СДВИГА

Математическая модель динамической пороупругости с тепловой релаксацией, сформулированная в разделе 2.3, описывает две моды Р-волн и одну S-волну. Уравнение (2.96) для S-волны наиболее просто, и для гармонических одномерных плоских волн

у/ = у/д ехр i{cot -рс), X= - -ids (5.57)

ему соответствует дисперсионное уравнение

/ [cl+cso+ioi в,с1) -<о{1 + ioi 9,) = О (5.58)

Соответственно для скорости поперечных волн Cs и коэффициента их затухания Ss получим следующие выражения:

- = -{.4" + ВГ; (5.59)

Ss = ~[A-Br, (5.60)

CsO ССО вр

Cso{csO + cL(0ef) --4,4 22 (5-62)

CsO CsooCO вр

Результирующие зависимости скорости и коэффициента затухания от частоты представлены на рис. 5.14 и 5.15 в безразмерном виде. 268

= 0.926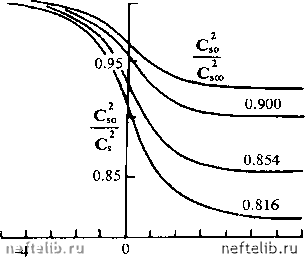

4 21nep(o

Рис. 5.14. Зависимость волновой скорости от частоты вследствие инерционно-вязкой диссипации

5s CsooQp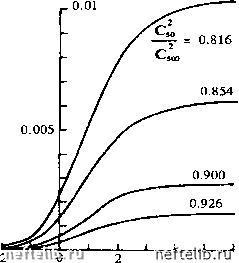

2 In ерш

Рис. 5.15. Зависимость коэффициента затухания от частоты вследствие инерционно-вязкой диссипации

5.3.2. ДВА ТИПА Р-ВОЛН

Система динамичесю1Х уравнений (2.88)-(2.94) для продольных волн весьма сложна, поскольку она учитывает одновременно взаимодействие сжимаемостей матрицы и самих твердых частиц, термические эффекты и, как и в случае S-волн, инерционно-вязкую релаксацию.

Если термический эффект достаточно слаб, а твердые частицы жестче чем матрица в целом, как, например, в случае водонасыщенных грунтов, то применима эффективная система (2.104). Существование двух типов Р-волн видно непосредственно, поскольку эффективные динамичесюе уравнения (2.104) отделены от (2.111).

Уравнение (2.105) для Р-волны первого типа отличается от уравнения (2.96) для S-волн только значениями волновых скоростей - "замороженной" и "равновесной".

Поэтому вполне аналогичное дисперсионное уравнение

/ (cl+cio+ico вр cl) -со(1 + ioi вр) = О (5.63)

применимо для волны порового давления:

р = Ро ехр i{cot - хх). (5.64)

Соответственно для Ср и Sp можно использовать графики рис. 5.14 и 5.15.

Первый тип волн характеризуется одинаковым направлением смещений твердых и жидких частиц. Однако смещения фаз противоположны (по знаку) в Р-волне второго рода. Тем самым жидкость должна покидать поры, чтобы полные деформации пористой матрицы были реализованы. Это приводит к весьма интенсивной фильтрационной диссипации, причем стандартное волновое уравнение заменяется на "телеграфное" уравнение (2.112).

Соответственно, дисперсионное уравнение Р-волны второго рода имеет вид

Zce/=ajef-i{p/po)\ (5.65)

где X - характерное волновое число деформаций матрицы: 270