Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 [ 5 ] 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284

1.5.3.3. Вращение твердого тела вокруг оси

Вид в плоскости гОМ.

Вид сверху.

к~ единичный вектор на прямой Л; 2 = Шс.

Vm = И лбм = n(/f л"5й) = n(/f лТШ)!/? л5й = ом,

sin а = нм =г

1.5.3.3.1. Момент инерции вращения

Для "точки" М массы т,:

оо/ =Ш л lui = рН л +"НМ л м)т Рассмотрим проекцию этого вектора на ось 6i:

5д; = ? • Оо/ = - (НМ л \?м)т, = m/}VM = m,n/f - кинетический момент относительно Л.

Для всего твердого тела:

г л г

Од = Jn, где = £m,,f = /"dm

- момент инерции относительно Л.

1.5.3.3.2. Пара вращения

Если вместо Vm рассмотреть Рм, получим аналогично составляющую на Oz (или Л):

странена на i 1ьно Л, или пар

2Wa = "ZnF,,

где сумма распространена на все твердое тело. Момент относительно Л, или пара, это:

Р, - составляющая, паргтлельная \?м (касательная), откуда

, <£1 , d% 2Кд = J- = Ja- - пара вращения. dt df

Следствие: вспм пара вращения равна нулю, тело находится в равномерном вращательном движении.

также называется динамическим моментом.

1.5.3.3.3. Теорема Гюйгенса

Пусть Aq - ось, параллельная оси Л и проходящая через центр тяжести G на расстоянии а от нее. Тогда Ja = Jq + Ma*. Следовательно, Jq минимально.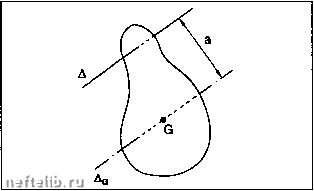

1.5.3.3.4. Количество движения

. . dVu rdJl . -.

Х= Х"-Г = Х"/[-аОМ + ПаУ„ .

Если скорость вращения постоянна, то

£Р, = £тДП А\?„) = - пХтД Результирующая центробежных сил есть вектор

При уравновешивании ротора, коленчатого вала:

- статическое уравновешивание (без вынужденного вращения) позволяет определить значение массы т, которую следует поместить на некотором расстоянии гот оси и найти плоскость, проходя1Чую через Л, в которой лежит вектор

£2*51 т,г, (черновое уравновешивание);

- динамическое уравновешивание позволяет определить перпендикулярную оси Л плоскость,

содержащую вектор Ст,г,, зная два вектора реакции на подшипники уравновешивающего механизма; оно позволяет также уточнить массу т в силу высокой чувствительности метода (О*).

1.5.3.3.5. Кинетическая энергия вращения

1.5.3.3.6. Работа сил, действующих на твердое тело

или, для любой другой точки Р тела:

5«=ХРм- (\?p+nA"Pra)df=: = • ХРмЛ + П • X ("РМ А Рм) dt,

и, по свойствам смешанного произведения:

m. = (ЯpV{+й%)dt.

Торсор внутренних сил равен нулю: он не работает в твердом теле.

Если торсор сил сводится к паре, Й = О и:

S&=йШdt = ЗЯdд,

S% = CdB

и мощность

3> = СП

1.5.3.4. Потенциальная энергия и механическая энергия

Когда работа силы Р между двумя удаленными моментами времени и ti зависит только от состояний в точках A{fi) и В{/2), говорят, что поле Р потенциально.

Таким образом:

Sg = Р. ЙЛ = F;,d)r + F/jy + Fd? = dig =-Л)

- полный дифференциал функции Щх, у, г), который не должен зависеть от времени.

н ,aur aur эи-

В частности, работа вдоль замкнутого контура равна нулю:

р. dM = О

(не так, как в случае сил трения).

Чтобы это было верно, должно выполняться условие rot Р = 0.

1.5.3.4.1. Потенциальная энергия системы

Пусть дана система, в которой внутренние силы потенциальны:

Ер = и + const - потенциальная энергия.

1.5.3.4.2. Обратимое преобразование

Скорости весьма малы, внутренние силы потенциальны, кажррв промежуточное состояние есть равновесие. Тогда, рассматривая силы связи как внешние силы, имеем:

mtn + неш = о для ВСЯКОЙ ТОЧКИ М,

откуда (wNi = <р: работа внешних сил полностью "восстановима".

Примеры:

5а = ид-Ув.

- пружина = 2 X - удлинение, к - жесткость;

- пружина, работающая на кручение: Ер - Св*;

- сила тяжести: Ер = mgz + const;

- центральная сила: Р проходит через фиксированную точку,

Р = KD и Ер = JKDdr.

1.5.3.4.3. Механическая энергия системы

dEc = de»vi + dm

d(Ec+Ep) = di8.

E = Ее + Ер - механическая энергия.

Если система изолирована: Е = const; потенциальные силы называются консервативными.

1.5.3.4.4. Потенциал, зависящий от времени

Пример: ребенок на качелях (маятник). Трением пренебрегаем:

Ер= mga( -cose),a = OG;

если OG = const, колебания периодичны, но меняя OG (а - переменно), можно изменять колебания.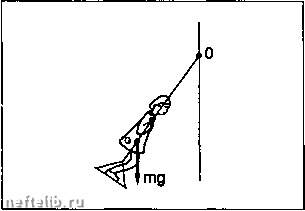

Маятник.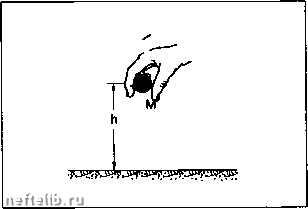

Работа, затраченная на по/тт М на высоту h, есть: W • mF-h - +Mgh. Погвнцналы1ая энергия массы Мувеличилась поэтому на Mgh.

Fs = + Mg

"1

Fs = -Mg

Ha массу M, находящуюся в покое на поверхности земли, действуют две равные и противоположив силы: Fg -гравитщюнная притяпюающая сила, F, - сила воздействия на М поверхности земли.

Если отпустить массу, потенциальная энергия U уменьшится, а кинетическая энергия увеличится, но их сумма останется постоянной на высоте х:

U(x)-Mgx

а на земле:

x = 0,v= J2gh.

Fq = - Mg

Чтобы поднять М с постоянной скоростью, надо приложить cnnyFm+Mg.

•то???;

Непосредственно перед касанием массы с землей вся потенциальная энергия, которую масса имела на высоте h, превратилась в кинетическую энергию.