Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 [ 8 ] 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284

Момент инерции относительно Л:

- 2pYly,-2Yal„-2apl,,.

** = J"!/ (/ + г) - момент инерции относительно Ох,

1у, = гп/уг - произведение инерции.

1.5.3.8.2. Эллипсоид инерции

в точке О твердого тела

Конец вектора = (X, Y,Z) пробегает по-

верхность с уравнением

I J<2 + \„У + 2\у,У2 - 21 - 2\У = 1.

Это эллипсоид с центром О, имеющий три оси симметрии, называемые главными осями инерции в точке О:

Ох„ Оуь Oz,. В системе Ox,/,z, эллипсоид имеет уравнение:

AX? + BY? + CZf = 1. Произведения инерции равны нулю. А, В, С - главные моменты инерции.

=а,Г, + Р,/,+У,А,, Й = П5 = (р, Q, /), J, = Aa? + Bp? + C7?,

1.5.3.8.3. Центральный эллипсоид инерции -в центре тяжести G

Главные оси инерции часто удобно находить из соображений симметрии.

с другой стороны, в точке О, расположенной на одной из этих осей:

l = £m;z;=Xm,CMz,=

= тдсс- + X,) Z, = CcZq +1,,,, = О,

GH = x,, ОН = х;.

Если О лежит на центральной главной оси, две другие главные оси в О параллвлы1ы централы4ым главным осям и

JA-J, + Ma2.

1.5.3.8.4. Центральный эллипсоид-эллипсоид вращения. Примеры семейств твердых тел

Твердое тело есть "стопка ломтикм;, центры тяжести которых расположены на оси Gz.

Для "ломтика" R:

£y,zm, = z£m,y, = О, T.e.Sz- главн£1я ось.

1.5.3.8.4.1. Каждый ломтик - это фигура,

для которой Gr является центром симметрии порядка л 3

Ломтик - совокупность материальных точек, расположенных в вершинах правильного многоуголь-

ника с е = -: п

!« = Х/= т/ Z COS* (а +W).

1 = Хх = т/ £ Sin*(а+W),

при любой ориентации а.

л-1 »-0

Зубчатая передача.

Турбина.

1.5.3.8.4.2. Каждый ломтик - зто один или несколько витков винта

Данному / соответствует один х> О и один х< 0.

Точно так же в О, только момент инерции С выделяется, А = В. Частный случай - тело вращения.

Червячная передача с двойной нарезкой.

1.5.3.9. Движение твердого тела с одной неподвижной точкой О. Общие уравнения

1.5.3.9.1. Кинетический момент относительно О

Система отсчета, составленная главными осями инерции, есть Ox,y,z,. Тогда

7, 7, /Г,

Р Q г

X Xi 1

Vu = П л ОМ =

OM л =

Pi/ + )-qxУ-rx,Z, Q(Z? + X?)-0,,-py,X, /•(X? + >) -pZ,X,-QZ,y,

Кинетический момент:

5o = "РМ л 7м = АрГ, + Bq7i + Сл?,, поскольку произведения инерции, такие как 5m,x,z, равны нулю. Замечание:

Точка О может быть центром тяжести.

Движение твердого тела с неподвижной точкой О.

1.5.3.9.2. Теорема о кинетическом моменте

V dt )

or Одг.у,*,

Oxyz

г J к

Р Q г Ар Bq Сг

Уравнения Эйлера:

Ар+(C-B)Qr=2JJo- i = L, Bq+(A-C)rp = Moh = M.

Cr+ (B-A)pQ = 2JJo- i = N.

1.5.3.9.3. Кинетическая энергия

E,= l(Ap? + Bqf + C = lJ,n

1.5.3.10. Свободное движение или движение Пуансо

Случай, в котором (Pn»ui) - О, и внешние силы проходят через О.

Замечание:

О может быть центром тяжести: свободное вращение тела вокруг центра тяжести.

Тогда:

9о = const

Е„ = 4й • 5о = const.

1.5.3.10.1. Тело, приведенное во вращение вокруг главной оси инерции

р=д = Оиг - const: вращение продолжается равномерно (вокруг главной оси 0..

Вес Р уравновешивает систему в состоянии покоя. Когда S приведено во вращение, последнее продолжается бесконечно долго при отсутствии трения.

Тем не менее, вращение вокруг средней главной оси инерции неустойчиво.

1.5.3.10.2. Тело, приведенное во вращение вокруг произвольной оси

Зо - постоянный вектор.

Eg = • Зо - постоянно, следовательно, ОН = - const.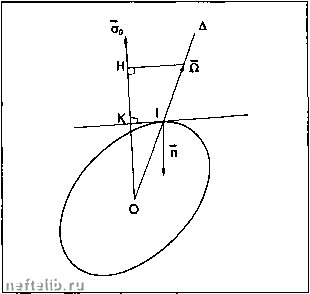

Й(р, Q, г) протыкает зллипсоид AX? + BVi + C2 = 1

/ р Q г

в I нормаль к зллипсоиду имеет направляющий вектор

он параллелен Зо. Наконец:

61. Зо = = 7. = const,

откуда 6R = const.

Плоскость Р, касательная к эллипсоиду в точке I, постояннее. Мгновеннс1я скорость в точке плоскости, лежащей на эллипсоиде, равна нулю (I лежит на мгновенной оси вращения А).

Движение твердого тела таково, что эллипсоид инерции в точке О вращается и катится без скольжения по фиксированной плоскости Р (определяемой начальными условиями).