Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 [ 9 ] 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284

1.5.3.10.3. Тело, у которого эллипсоид

инерции есть эллипсоид вращения

с осью 0Z

В = А

Точка I описывает окружность IJ на эллипсоиде и окружность 1Г на плоскости Р.

Конус IOJ с осью Oz, катится без скольжения по фиксированному конусу ЮГ с осью 9о> о постоянной скоростью а.

Имеем: г = const = Гд (3-е уравнение Эйлера) и р = р cosot,

q = р sincot,

0) =

1.5.3.10.4. Относительное движение вокруг центра тяжести

Если на тело действуют внешние силы, проходящие через G, система uxyz смещается параллельно самой себе.

Движение точки G дается теоремой количества движения:

Движение вращения вокруг G происходит "по Пу-ансо":

- кинетический момент относительно G:

= iSJJeCF) = о.

киивтмчвскэя эноргия.

откуда:

кА = const.

Снаряд нарезного орудия

Здесь предполагается, что сила сопротивления воздуха проходит через G.

1.5.3.11. Задача Лагранжа. Движение волчка

Внешние силы не проходят через 0:

Углы Эйлера (международное соглашение) 1.5.3.11.1. Вращение волчка

1.5.3.11.1.1. Плоскость zOx вращается вокруг 6z \jf - угол прецессии, бх - On: узловая ось, Оу -" Ол,: прецессия Шр=к.

1.5.3.11.1.2. Плоскость zOn вращается вокруг Gn, узловой оси

бл, -►Oiv

Sz-► SZ

9-угол нутации,

нутация - &ц = ёл

1.5.3.11.2. Плоскость иЮл вращается вокруг

Ф - угол собственного вращения, бл-►Ох, 6w-►бу, Собственное вращение: S„ = q>F, .

1.5.3.11.3. Движение волчка

а = у+6?7+ф, - мгновенное вращение. Волчок неподвижен в системе Ox,y,z, и:

f = sin в (sin ф • Г, + cos ф • /,) + cos е-rf = cos ф • Г, - sin ф • /, Составляющие П в системе Ox,y,z,(R,) таковы:

Р = У sin 6 sin ф + 6 С08ф Q = у sin 6 COS ф - 6 8iПф Г= у С08в + ф

Напомним уравнения Эйлера:

Ар+ (C-B)Qr=3Ko- 1 = L Bq+ (a-C)fp = aRo-7i = m Cf+ (В-А)р(7 = 2йо- 1 = N

Поскольку на волчок действует вес rriS, имеем:

Slio > mga sin 6 (cos ф • /j - sin ф • /,).

В силу его вращательной симметрии А > В, откуда:

Ар+ (C-a)Qf= тда sin 9 cos ф

Aq+ (а-С)ф = -тда sin 6 cos ф LCf=0

Эта система допускает три следующих первых интеграла:

Ф + V cos е = = const;

сохранение кинетического момента относительно бг о, * do • к дает:

сохранение механической энергии:

Е = Ео+Ер = (Ap + Aq + сЛ +mgz = const, откуда:

Е= A(v* sin*e + e*) +C/J + mga cos 9 = const.

Движение волчка зависит от начальных условий.

Исследование показывает, что угол нутации заключен между двумя значениями 6, и Bj. произвольная точка оси волчка описывает на сфере с центром О кривую, которая может иметь различные формы.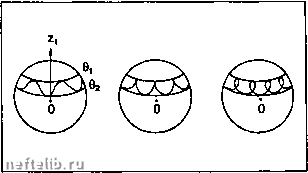

Траектория подвижного конца волчка

1.5.3.11.4. Гироскоп Чем больию начальное вращение Фо, тем ближе

друг к другу е, и 02.

Впрочем, в этом случае

6 - const.

Нутационное движение пренебрежимо, и:

П7£а py,pQQKonH4ecKoe приближение. Сфо

ст, = a\jf sin*e+Cfo COS е = CfoK

постоянно, поскольку (65 лтф-к = 0;

Пример гироскопа. Гчроскопичвский волчок

гчроскопичвский эффект.

Гироскопический эффект:

Вначале система уравновешена весом Р, лишь S вращается вокруг своей octi Если подействовать на нее горизокгальной силой F с помощью палочки D, то момент вертикален; конец приобретет скорость, параллельную 92о и имеющую то же направление: это прецессионное движение.

Обратно, всякое изменение начального движения вызывает пару Щ-

1.5.3.11.5. Применения гироскопа

Гироскоп используется в качестве:

- стабилизатора пути; например, он позволяет регулировать направление движения торпеды,

- нейгтрализатора боковой качки,

- компаса; в г11роскопичвском компасе О не совпадает с G. Если он отклоняется от направления на север, появляется сила Кориолиса, дающая противоположный гироскопический эффект. Следовательно, появляются колебания, которые надо погасить.

гироскоп, смонтированный на арматуре S. Точка О i центр тяжести. Если поворачивать S", прилагая момент i направленный вверх, г, получает скорость, направленную вверх: прецессионное движение.

Навигация с помощью гирокомпаса.

1.5.3.12. Моменты инерции распространенных линий, поверхностей и объемов

Выдержки из "Техники инженера