Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 [ 100 ] 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121

ординатах Х = In

нн - 1 sho

С увеличением проницаемости подвижность нефти увеличивается, что приводит к уменьшению остаточной нефтенасыщенности, поэтому параметр S является возрастающей функцией проницаемости. Аппроксимируя ее степенной зависимостью 5 = Xk, получим окончательно

откуда

где X, (7 - эмпирические коэффициенты (сг > 0), определяемые по данным исследований кернов. Отметим, что зависимость (5.26) спрямляется в ко-

s-H/2 , X = Ink:

Х = \nX + oX. (5.28)

Используя (5.28), легко найти InX и с обычным методом наименьших квадратов.

Как видим, использование априорной информации существенно упростило модель, позволив с помощью всего лишь двух эмпирических коэффициентов (вместо трех в (5.22)) учесть еще и зависимость коэффициента вытеснения от начальной нефтенасыщенности.

Это позволяет компенсировать недостаток экспериментальной информации и получить обоснованные расчетные формулы по ограниченному объему лабораторных данных.

В принципе, модель (5.26) можно уточнить, считая показатель степени p в (5.23) неизвестным и определяя его одновременно с X и ( .

В любом случае опыт показывает, что значение р =1- является хорошим

первым приближением.

В заключение приведем пример еще одной априорной оценки: опытному специалисту сразу ясно, что возможные значения показателя степени в уравнении (5.26) ограничены неравенством

7< 1. (5.28)

Это следует из того, что одни и те же изменения проницаемости проявляют себя неодинаково на различных участках шкалы проницаемостей. Поэтому проявления проницаемости часто нелинейны, вместо k мы воспринимаем результат нелинейного сжатия, которое можно описать операциями k Igk или k k7, где 0 < с < 1. Не зря в зависимостях, связывающих проницаемость с объемными характеристиками пласта, фигурирует lg k (см., например, (5.22)).

Подчеркнем, что априорные оценки типа (5.28) имеют исключительно важное значение как средство контроля и повышения устойчивости расчетов при решении задач восстановления зависимостей по выборкам малого объема.

В работах [13, 14] зависимость остаточной нефтенасыщенности от начальной предлагается аппроксимировать выражением

и 2 sHH + sHH m

пористость, (р, в - эмпириче-

1 + нн

где V - средняя скорость фильтрации, m ские коэффициенты.

По форме это соотношение также представляет собой Паде-аппрок-симанту. Поскольку скорость фильтрации пропорциональна проницаемости, то оно позволяет учесть и зависимость остаточной нефтенасыщенно-сти от проницаемости. Но структура этой аппроксиманты не во всем удовлетворяет сформулированным нами априорным представлениям.

0,70

0,65

0,60

0,55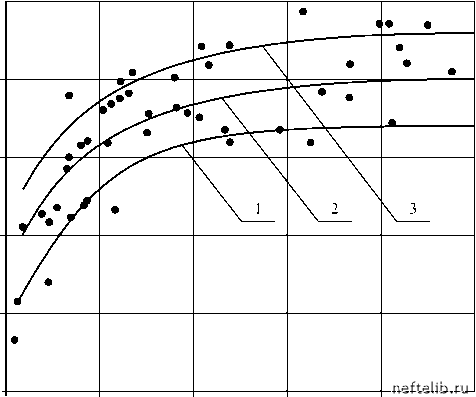

1200

k, мД

Рис. 5.10. Зависимость коэффициента вытеснения от проницаемости

при различных sHH.

• - экспериментальные точки, 1 - sHH = 0,5 , 2 - sHH = 0,65, 3 - sHH = 0,85

5.3. Метод асимптотических координат

Положим, что имеется некоторая величина F , зависящая от двух параметров p и q. Пусть в условиях эксперимента задавались определенные

значения параметра q = q1, q2, q3,...,qn и определялась зависимость F от p при фиксированных q. В том случае, когда вид полученных кривых в плоскости (p,F )носит качественно сходный характер, часто удается подобрать специальные координаты, с помощью которых исследуемую сложную двумерную поверхность F = F(p, q) удается описать с помощью нескольких более простых плоских кривых (при этом семейство кривых в плоскости (р - F), соответствующих различным значениям q, сжимается в одну универсальную кривую).

В качестве примера рассмотрим экспериментальные зависимости дебита жидкости Q от расхода газа V и диаметра подъемника d , полученные [15] на лабораторной установке, моделирующей работу газлифтной скважины (см. рис. 5.11).

Перейдем к переменным

x = V(-0(d()), (5.30)

Vm(d)-V0(d)

y = Q

Qm (d У

где V0(d ) - расход газа, при котором начинается подъем жидкости (Q - 0 при V - V0), Vm (d) - расход газа, соответствующий максимальному дебиту жидкости Qm(d ).

Тогда все пять кривых на рис. 5.11 можно представить в виде одной универсальной зависимости y = f (x), показанной на рис. 5.12. Характер-

Пример. Обработка данных исследования кернов одного из пластов Нефтеюганского региона по описанным выше алгоритмам привела к зависимости

S = s«« (5 29)

"° 1+k0,15 s;,!2

где проницаемость измеряется в миллидарси. В этом случае, действительно, 7 = 0,15 < 1.

На рис. 5.10 приведены графики функций в = e(k), полученные с

использованием (5.29), при shh = 0,5, shh = 0,65 и shh = 0,85 (кривые 1, 2

и 3 соответственно). Как видим, большой разброс значений коэффициента вытеснения при фиксированных значениях проницаемости, наблюдающийся при проведении лабораторных исследований, можно объяснить влиянием начальной нефтенасыщенности.