Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 [ 99 ] 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121

0,9 -

0,8 -

0,7 -

0,6 -

0,5 -

0,4 -

0,3 -

0,2 -

0,1 -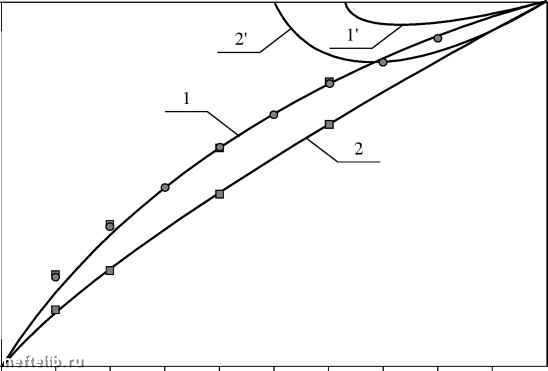

0,1 0,2 0,3 0,4 0,5

0,6 0,7 0,8

Рис. 5.8. Зависимость коэффициента совершенства скважины от степени вскрытия пласта

В настоящее время при проектировании используются осредененные статические зависимости, устанавливающие связь коэффициента вытеснения с параметрами, определяющими фильтрационно-емкостные свойства пласта и условия вытеснения нефти водой. Часто в проектах разработки месторождений Западной Сибири применяют корреляции, связывающие коэффициент вытеснения с проницаемостью пласта k, в виде

в = а Ig2 k + b Ig k + c,

(5.22)

где a, b, c - эмпирические коэффициенты, определяемые из данных лабораторных исследований кернов [12]. При этом пласты различных месторождений объединяются в несколько групп (АС, ВС и т. д.), внутри которых для всех объектов разработки принимается зависимость (5.22) с одними и теми же коэффициентами.

Подобный усредненный подход был оправдан в период массового ввода в разработку крупных месторождений с хорошими фильтрационными характеристиками. Однако в настоящее время, когда осваиваются площади с трудноизвлекаемыми запасами, необходимо увеличить надежность технологических решений за счет повышения точности расчетов.

В связи с этим обоснование коэффициента вытеснения необходимо производить индивидуально для каждого пласта. Но при этом объем экспериментальных данных, используемых для оценки эмпирических коэф-

, (5.23)

1 + S SS„

фициентов, резко уменьшается, поскольку при выводе корреляционных зависимостей должны привлекаться только результаты исследований, проведенных на кернах рассматриваемого объекта.

Требуется также уточнение модели (5.22), поскольку в водонефтя-ных зонах залежей коэффициент вытеснения нефти зависит не только от проницаемости, но и от начальной нефтенасыщенности пласта [13, 14] (зависимости в = e(k) применимы только в чисто нефтяных зонах, начальная нефтенасыщенность которых определяется насыщенностью связанной водой, хорошо коррелируемой с проницаемостью). Если идти по пути усложнения зависимости (5.22) путем введения новых членов, зависящих от shh , то это еще более усугубит проблемы, связанные с нехваткой данных для определения большого числа эмпирических коэффициентов.

Эти затруднения могут быть преодолены за счет более осмысленного выбора класса функций, в котором ищется зависимость в = в((,shh). Структура идентифицируемой модели должна явным образом учитывать априорную информацию о механизмах вытеснения нефти водой. (Вообще говоря, это является универсальным рецептом: структура пробных функций в задачах восстановления зависимостей должна быть подобрана с учетом особенностей моделируемых процессов.) Прежде всего, обратим внимание на то, что, с точки зрения подземной гидродинамики, более правильно ставить задачу определения не коэффициента вытеснения, а остаточной нефтенасыщенности как функции проницаемости и начальной неф-тенасыщенности sho = f (k, shh ). Коэффициент вытеснения есть величина

вторичная, зависимая; она полностью определяется значениями shh и sho .

Отметим, что в современных гидродинамических пакетах программ, предназначенных для моделирования процессов разработки, коэффициент вытеснения напрямую вообще не используется: он закладывается в модель лишь косвенно, путем задания значений shh и sho (shh определяется как

критическая нефтенасыщенность, при которой фазовая проницаемость нефти становится равной нулю). Последнее не означает, однако, что нужно вообще отказаться от такого понятия, как коэффициент вытеснения. Эта величина является важной интегральной характеристикой, привычным контрольным параметром, с помощью которого можно судить об адекватности расчетов.

На рис 5.9 представлен типичный вид зависимости остаточной неф-тенасыщенности от начальной (точками показаны результаты одной из серии лабораторных экспериментов, проведенных на кернах с близкими значениями проницаемости). Будем искать ее в виде обобщенной (допускающей дробные степени) Паде-аппроксиманты

где a, в, S - коэффициенты, в общем случае зависящие от проницаемости, p - некоторое постоянное число, 0 < р < 1.

Приведем априорные соображения о поведении зависимости sHO = sHO (sHH) вблизи нуля и единицы.

При малых значениях нефтенасыщенности нефть оказывается защемленной в порах капиллярными силами и вытеснить ее не удается. Поэтому при sHH 0 sHO ~ sHH или

sho = shh + 0(s2H ), (5.24)

т. е. кривая sHO (sHH) в точке sHH = 0 касается биссектрисы.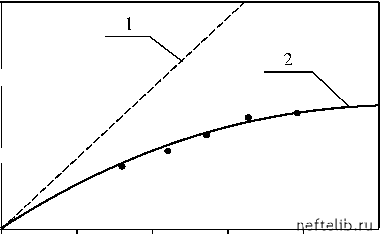

Рис. 5.9. Зависимость sHO от sHH при постоянной проницаемости • - экспериментальные точки; 1 - прямая sHO = SHH, 2 - Паде-аппроксимация зависимости sHO от sHH по формуле (6.26).

При малых sHH

1+ S

что при подстановке в (5.23) дает

sho -a-aS sSh +7 shh-7S s]+h...

(5.25)

Приравнивая первые члены разложений (5.24) и (5.25), получим a = 0, 7 = 1.

При увеличении sHH график зависимости sHO от sHH быстро отходит от прямой sHH = sHO и выполаживается, стремясь к параболе sHO =1 s

(см. рис. 5.9). Для определенности положим 1 - р = -, откуда р = -.

.1-p