Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 [ 46 ] 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121

AP, МПа

0,30 -0,25 -0,20 -0,15 -0,10 -

0,05

0,00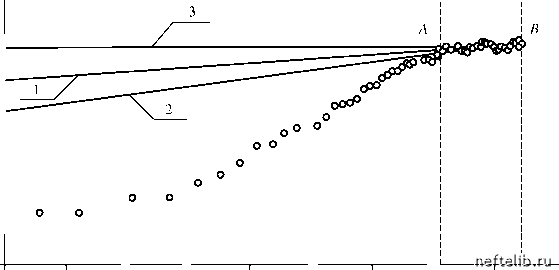

In t

Рис. 2.9. Результаты численного эксперимента по наложению «шума»

Для того чтобы смоделировать эту ситуацию нами, был проведен математический эксперимент, в ходе которого исходная выборка замеров {AP(tl)} заменялась на выборки, полученные путем наложения на прямую 1 случайных «шумов». При этом методом Монте-Карло моделировались равномерно распределенные ошибки величиной порядка 1%.

На рис. 2.9 прямыми 2 и 3 ограничена область, в которой лежат прямые, полученные по таким модельным выборкам. Как видим, малые ошибки в определении AP приводят к значительным ошибкам в определении фильтрационных параметров пласта (например, разброс значений £ составляет 200%).

Если обратиться к расчетным формулам (2.66), то становится ясно, что отмеченная неустойчивость вызвана малостью знаменателя Dx, т. е.

малостью длины спрямляемого участка. Малые ошибки, содержащиеся в числителях уравнений (2.66), возрастают за счет деления на величину Dx,

близкую к нулю. Иными словами, желание провести прямую через «облако» точек приводит к плохо обусловленной системе уравнений.

2.6.2. Регуляризирующий метод обработки КВД

Итак, задача интерпретации КВД по методу МДХ является некорректно поставленной. Для повышения устойчивости ее решения необходимо привлечь методы регуляризации некорректных задач, заключающиеся в том, что на искомые параметры накладываются дополнительные ограничения, вытекающие из некоторых априорных соображений.

x2 ) + а

При обработке КВД в качестве такой априорной информации могут выступать оценки величины коэффициента гидропроводности, полученные предварительно другими методами. Например, коэффициент гидропровод-ности можно рассчитать, оценив среднюю проницаемость пласта по данным геофизических исследований и отборам керна. Полезную информацию могут дать также данные нормальной эксплуатации скважины (гидро-проводность можно оценить по формуле Дюпюи, зная дебит и задавшись некоторыми примерными значениями депрессии и скин-фактора).

Пусть E0 - предварительная (размерная) оценка коэффициента гид-

ропроводности, полученная одним из перечисленных выше методов. Эта информация может быть формализована в виде требования минимизации функционала

0(a )=(a - a0 )2, (2.67)

где a0 = (величина a в (3.52) уже безразмерна). E0

Таким образом, задача становится двухкритериальной - требуется найти такие значения a и b , при которых функционалы (2.65) и (2.67) становятся как можно меньше. Переходя к однокритериальной постановке, сведем эту проблему, согласно разделу 2.2, к минимизации регуляризи-рующего функционала

M (a, b )= I (a, b ) + а0(a), где а - параметр регуляризации (а > 0).

Ясно, что чем больше значение а, тем более устойчивым является решение.

Легко показать, что значения a = a и b = b , доставляющие M (a,b) минимум, определяются соотношениями

~ = (x. + аao Ч{y ; (2.68)

Как видим, в знаменателях дробей появилось положительное число а , что устраняет деление на малое число Dx и делает задачу устойчивой.

Как уже отмечалось в разделе 2.5, описанный алгоритм устойчивой оценки параметров можно назвать регуляризирующим методом наименьших квадратов (РМНК).

Величина а определяется из принципа невязки

Iа(a,b) DP,

где Iа(aг,b) - значение невязки (2.65), полученное при данном значении а , DP - дисперсия ошибок измерения давления.

Для определения значения параметра регуляризации может быть предложен и другой подход. Задаваясь различными возрастающими значениями а, при каждом из них проводят описанный выше математический эксперимент, рассматривая разные выборки замеров {AP(t)}, «приготовленные» методом Монте-Карло, и оценивая соответствующий разброс искомых параметров. За оптимальное значение принимается значение а , при котором относительная ошибка определения a и b достигает заданной величины. Такой алгоритм определения параметра а может быть назван принципом Монте-Карло.

Пример расчетов

Изложенная методика была использована при интерпретации рассмотренной выше КВД.

Привлекая данные ГИС и информацию о вязкости нефти, мы получили априорную оценку гидропроводности £0 = 3,80м3/Пас. Дебит скважины в пластовых условиях до ее остановки был равен Q0 = 70 м3/с. Мощность пласта составляет h = 8,2 м, сжимаемость пластовой системы

в = 12 10-4 МПа-1. При обезразмеривании исходных данных мы положили £* =£0. В табл. 2.13 приведены результаты применения РМНК к обработке КВД при различных значениях а .

В четвертом и пятом столбцах этой таблицы приведены относительные ошибки определения величин £ и S. Здесь о£ и Gs - среднеквадратичные отклонения от средних для оценок £ и S, полученные в численных экспериментах по наложению 1%-го «шума» на исходные замеры. В шестом столбце приведена величина

характеризующая относительное увеличение невязки I при увеличении параметра регуляризации а . Здесь I 0 - невязка, полученная по МНК, т. е. при а= 0.

Таблица 2.13

Обработка КВД регуляризирующим методом