Главная  Переработка нефти и газа 

Скачать 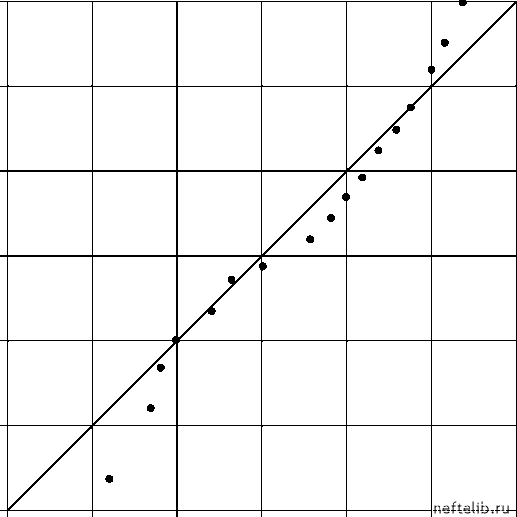эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 [ 95 ] 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121

Угр, М /сут.

700 Уг, м3/сут.

Рис. 5.2. Сравнение расчетных и действительных значений расхода газа

Этот простой пример показывает, что идеи безэталонного измерения могут быть использованы для повышения точности замеров с помощью приборов с грубой шкалой.

Пример 3. Определение проницаемости по данным геофизического исследования скважин (ГИС)

Основные трудности при создании трехмерных гидродинамических моделей нефтяных месторождений связаны с определением распределения проницаемости по глубине. Гидродинамические исследования скважин и данные нормальной эксплуатации (т. е. данные о продуктивности скважи-

ны) позволяют оценить только среднюю по мощности пласта проницаемость

1 h h 0

где k(z) - проницаемость горных пород на глубине z (отчет идет от подошвы пласта), h - толщина пласта.

Восстановить функцию k(z) по данным исследования кернов невозможно, поскольку это требует огромного объема лабораторных исследований, да и обеспечить достаточно полный вынос керна затруднительно.

Прямое определение проницаемости по каротажным кривым, снимаемым в ходе геофизических исследований скважин, также невозможно, поскольку они позволяют оценить только объемные характеристики (такие как пористость, насыщенность), а проницаемость является динамической, не объемной характеристикой. В этом смысле каротажные кривые похожи на мгновенный фотоснимок: если сфотографирован бегущий по улице человек, то по одному снимку можно оценить его массу (объемную характеристику), прикинув рост бегуна путем сравнения с высотой домов, но скорость бега (динамическую характеристику) можно найти, только оценив пройденную дистанцию по двум снимкам, снятым в разные моменты времени.

Несмотря на это, предпринимаются попытки оценить проницаемость по каротажным кривым косвенным путем, определив сначала по данным ГИС пористость и насыщенность связанной водой se , а затем привлекая корреляционные зависимости вида k = p{m, se ). Так, часто используют соотношения

k = , (5.6)

где A, а и в - эмпирические коэффициенты [7].

Однако погрешность таких оценок весьма велика. Тем не менее корреляции, подобные (5.6), верно отражают качественную тенденцию (рост проницаемости с увеличением пористости и уменьшением насыщенности связанной водой). Это наводит на мысль использовать соотношения вида (5.6) в качестве компараторов, с помощью которых можно ранжировать неизвестные значения проницаемости. А для количественной оценки проницаемости можно использовать метод безэталонных измерений.

Принято считать, что проницаемость является случайной величиной, распределенной по логнормальному закону. Эта информация может быть использована при вычислении математических ожиданий порядковых статистик. Неизвестные параметры распределения (математическое ожидание и среднеквадратичное отклонение), свои для каждой скважины, могут быть

определены по замерам проницаемости керна, а также по значениям средней проницаемости km, оцененным исходя из данных гидродинамических

исследований или нормальной эксплуатации скважин. Детали расчетов, в силу их очевидности, мы здесь не приводим.

5.1.3. Безэталонная идентификация

Многие задачи идентификации можно представить в виде проблемы «черного ящика», на вход которого подается сигнал x , а на выходе наблюдается отклик y. Измеряя различные значения xi и соответствующие им

значения yi, по выборке {xi,yi}, i = 1,2,...,n, восстанавливают функциональную зависимость y = p(x) (см. рис. 5.3 а). Как видим, в классической

схеме идентификации предполагается наблюдаемость (измеряемость) входа и выхода.

Однако описанная выше процедура безэталонных измерений позволяет поставить совершенно новую задачу идентификации: определение характеристик «черного ящика» с ненаблюдаемым входом [1].

Это возможно при выполнении следующих двух условий:

- входной сигнал x представляет собой случайную величину с известным законом распределения (см. рис. 5.3 б);

- зависимость y = (p(x) монотонно возрастает или монотонно убывает.

Последнее условие означает, что величина y может служить компаратором, необходимым для ранжирования значений x.

измерительный прибор

"черный ящик"

Рис. 5.3. Схема идентификации