Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 [ 68 ] 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121

щий иллюстративный расчет. Перепишем (3.62) в безразмерных переменных, приведя его к виду

y(t)

y(t) = x(t) + a 2mL • P2

2 Q(t), x(t)

- t -т АР 2

х(т)-т , 2L2 D

(3.63)

k P22 3l

Положим a = 1, что является реальным значением. Пусть x(t) изменяется ступенчато через интервал времени Т2 = 0,1Т1. Поскольку течение квазистационарное, примем, что период времени Г2 также значительно

превышает гидродинамическое время установления режима. При этом в течение времени наблюдения на одном режиме расход Q(t) меняется не

более чем на 7-8%, что находится в пределах погрешности обычных экспериментов на керне. Таким образом, формально традиционная методика экспериментальных исследований выполняется. Тем не менее вид зависимости Q -АР определяется в данном случае последовательностью изменения перепада давления. На рис. 3.9 представлены расчетные зависимости, полученные при увеличении (кривая 1) и уменьшении (кривая 2) перепада давления. В первом случае полученная зависимость характерна для двучленного закона фильтрации.

5 4 3 2 1

0 1 2 3 4 5

Рис. 3.9. Расчетные зависимости q от АР :

1 - при увеличении перепада давления,

2 - при уменьшении перепада давления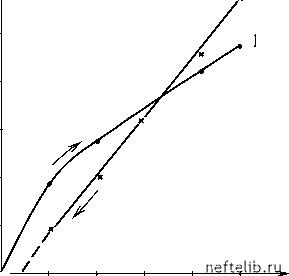

На рис. 3.10 эта зависимость перестроена в координатах--y, как

это обычно делается для проверки справедливости двучленного закона. Вторая зависимость на рис. 3.9 соответствует закону фильтрации с начальным градиентом давления. При немонотонном изменении депрессии зависимость может иметь различный вид (например, 5-образная кривая). Кроме того, если по полученным данным определить коэффициент продуктивности (проницаемости) керна, это значение будет кратно отличаться от истинного.

Более сложная ситуация возникает, когда фильтрация газа происходит в неоднородной среде. Пусть, например, в составе пористой среды имеются низкопроницаемые включения, в частности глинистые. Известно, что движение газа через глину начинается при создании определенного критического начального градиента давления. В этом случае газ, сорбированный породой в низкопроницаемых зонах, при снижении давления выделяется не сразу, а после достижения определенного перепада давления между низко- и высокопроницаемой частями и, наоборот, - при повышении давления. При этом фильтрация газа происходит по высокопроницаемой части. Таким образом, рассматриваются две равномерно перемещенные среды с различными параметрами. В соответствии с этим в первом уравнении системы (3.49) поток f представляется в виде двух слагаемых:

f = f1 + f2 , где f1 - поток десорбируемого газа из высокопроницаемой

среды, f2 - то же из низкопроницаемой.

1,0 0,8 0,6 0,4 0,2J

Рис. 3.10. Расчетные зависимости q от AP

Величина потока f1 подсчитывается по формулам (3.55) и (3.57). При определении потока f2 следует учесть наличие критического перепа-

да давления АР0 между низко- и высокопроницаемыми частями пористой среды. Это можно сделать, представив поток f2 в виде (см. (3.57)):

а) при снижении давления

- (1 -m) \F2(t -т)[а2Р(т) + АР0) - С1 2)]-т -t

f2 = s(1 - m)q2 = при P1 - P > АР0,

(3.64)

0 при 0 < P1 - P <АР0,

б) при повышении давления

- (1 - m) s -t \ F2 (t - т)[а2 (Р(т) - АР0) - С1,2)]-т

f2 = jnpn P - P1 >АР0,

(3.65)

0 при 0 < P - P1 <АР0. Функция F2 совпадает с определенной выше функцией F с точностью до значений параметров. Повторяя вывод уравнения (3.62), легко получим выражение для расхода Q(t ) в данном случае:

2МР0 L

АР 2 (t) +

+ 2в2 L2 D2

2e1L2 D1 t 3l1

АР 2 (т)-т +

(3.66)

t -т

(АР2(т) -г)-т

где индексы 1 и 2 относятся, соответственно, к высоко- и низкопроницаемым частям пористой среды.

Последнее слагаемое в правой части (3.66) обращается в ноль

АР 2

< Y. Как следует из (3.66), при достижении определенного пере-

пада давления на зависимости Q(t) = Q[АP (t)] будет наблюдаться излом,

что подтверждается результатами экспериментальных исследований.

Рассматриваемая модель допускает обобщение на случай полидисперсной пористой среды, состоящей к тому же из разнородного материала. В этом случае каждый компонент пористой среды обладает своими физико-химическими и геометрическими параметрами: - li, Di, Г, Г1 i. С учетом этого соотношение (3.61) примет вид

Q(t)

2МР0 L

АР2(t) + - (t -т)АР2(т)-т , -t

i=10

(3.67)