Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 [ 72 ] 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121

Приведенная постановка задачи может быть упрощена с учетом малости параметра е (т. е. фактически малости массы жидкости в зазоре).

Пренебрегая в (3.93) членом е-, получим

v(S)-= const.

Решение этого уравнения неединственно. Оно может быть сконструировано как совокупность пространственных структур - «доменов», представляющих собой области с различными значениями концентра-

ции Si и скорости сдвига

(концентрация и скорость сдвига внутри

каждого «домена» не зависят от п) [3, 61]. При этом граничное условие (3.95) выполняется, если

Hi = 1 -

S Hi = 1,

где N - число «доменов», Hi - толщина i-го домена.

Тогда система уравнений в частных производных (3.93)-(3.97) сводится к нелинейной динамической системе вида

d 2 X dt2

-AB + FX = 0,

N H.

= -Si + A

1 - exp

t=1y(Si) - GSiB

<Si)

v(Si )= p + exp(- Si1).

Исследование этой системы было проведено нами численно при следующих значениях параметров: N = 2, Л = 25, F = 17, A = 4, р = 0,1,

Hi = H 2 = 0,5, 1 = 10. Рассматривалось влияние величины безразмерной

скорости сдвига EE = 4g на характер движения системы.

Результаты расчетов суммированы на рис. 3.11, где показана зависимость безразмерного касательного напряжения Г от Ee .

Эта зависимость характеризует положения равновесия рассматриваемой динамической ситемы, к которым, в случае устойчивости, решение стремится с течением времени. На рисунке эти устойчивые ветви отмечены жирными линиями. При малых значениях скорости сдвига ( Ee < 0,95) структурные связи в жидкости не разрушаются. Имеет место простое сдвиговое течение жидкости с большой вязкостью, в которой не происходит

разрушения поля течения на доменные структуры. Если в начальный момент времени по каким-либо причинам часть структурных связей нарушена, т. е. Si (0)ф 0, то эти разрушенные связи со временем полностью восстанавливаются.

0,45

0,22

0,00

0,82

1,63

Рис. 3.11. Зависимость Т от E

С увеличением скорости сдвига (ti > 0,95) происходит разделение поля течения на «доменные» структуры с разрушением части связей вблизи подвижной стенки. При этом нулевое состояние S[ = 0 теряет устойчивость с рождением нового положения равновесия Ф 0, которое, в свою

очередь, при дальнейшем увеличении tt теряет устойчивость с образованием предельного цикла. Размах колебаний величины касательного напряжения (Tmax и Tmin) показан на рис. 3.11 пунктирными линиями.

Средние по времени значения Т при этих колебаниях изображены тонкой сплошной линией.

При дальнейшем увеличении скорости сдвига tt имеет место процесс последовательного удвоения периода автоколебаний, приводящий к хаосу при it = tt0 = 1,517. Наблюдающиеся при этом стохастические колебания величины касательного напряжения показаны на рис. 3.12.

Анализ соответствующего этому аттрактору отображения Лоренца (связи между последовательными экстремумами напряжения, рис. 3.13) показывает, что в исследуемой системе переход к хаосу реализуется по

классическому сценарию Фейгенбаума. Об этом свидетельствует также то, что значения параметра En , при которых происходит удвоение периода, подчиняются закону Фейгенбаума:

Gn - G

где в данном случае С = 6,54.

0,41

0,27 -

0,14

0,00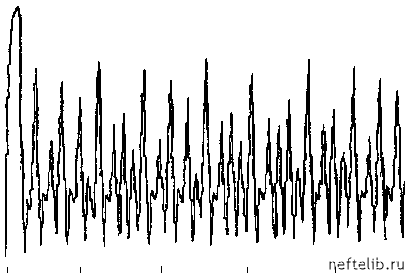

14,4

21,6

28,8

Рис. 3.12. Хаотические колебания касательного напряжения

s1(n+1) -

1,78-

1,45h

1,13-

1,13

1,45

1,78

Рис. 3.13. Одномерное отображение