Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 [ 47 ] 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121

Оптимальным признается значение а= 0,50, при котором относительная ошибка определения E и S порядка 3%. При этом значении а £ = 3,93 (E = 13,0 м3/Пас) и S = 3,45.

Сравнивая значения при а = 0,50 и а = 0 видим, что учет априорной информации не приводит к заметному увеличению невязки.

На рис. 2.10 показан разброс положений прямой a ln t + b, вызванный наложением «шумов» на исходные данные, при применении РМНК с а= 0,50. Наглядно видно, что устойчивость решения обратной задачи значительно повысилась.

Таким образом, интерпретация КВД не должна быть ограничена простым расчетом фильтрационных параметров по готовым формулам. Необходимо исследовать полученные результаты на устойчивость, для чего рекомендуется провести численные эксперименты по наложению на исходные данные «шумов», моделирующих случайные ошибки измерений. Если численный эксперимент покажет, что при данном качестве исходной информации результаты расчетов неустойчивы, необходимо использовать регуляризирующие (повышающие устойчивость) алгоритмы, заключающиеся в привлечении априорной информации о пределах, в которых могут лежать искомые параметры.

AP, МПа

0,30 -

0,25 -

0,20 -

0,15 -

0,10 -

0,05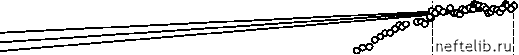

0,00

I шХ

оооО

о о

о о

ln t

Рис. 2.10. Результаты численного эксперимента по наложению «шума»

с регуляризацией

2.7. Оценка извлекаемых запасов нефти на основе феноменологических моделей

Как правило, нефтяные месторождения России эксплуатируются с применением заводнения. В настоящее время существует множество мето-

дов оценки начальных извлекаемых запасов (НИЗ) для таких месторождений по характеристикам вытеснения - зависимостям накопленного отбора нефти от накопленного отбора жидкости, представленным в той или иной

форме [28-34].

Как и любые задачи долгосрочного прогноза, экстраполяция промысловых данных этими моделями очень чувствительна к малым погрешностям, содержащимся в исходной информации. Поэтому большое значение имеет обоснованный выбор вида уравнений, аппроксимирующих динамику накопленной добычи нефти.

Для устойчивой оценки НИЗ могут быть использованы эволюционные модели, основанные на универсальном законе роста сложных природных систем - логистическом уравнении [35]. В рамках этого подхода устойчивость долгосрочного прогноза обеспечивается за счет привлечения априорной информации об универсальных законах развития. Здесь легко прослеживается аналогия с некорректно поставленными задачами, регуляризация которых также производится с помощью априорной информации.

Многочисленные примеры из разных областей наук показывают, что эволюции сложных систем присуще свойство самоподобия. В связи с этим в настоящем разделе рассмотрены возможности применения в задачах прогноза добычи нефти модели С. П. Капицы [36], описывающей самоподобный (автомодельный) рост.

Обычная практика применения прогнозных моделей подразумевает их «обучение», т. е. подбор «наилучших» параметров моделей из условия минимального отклонения расчетных кривых от экспериментальных точек. При этом широко используется метод выравнивания - переход к некоторым специальным координатам, в которых характеристики вытеснения линеаризуются относительно искомых параметров. Однако это преобразование приводит к появлению систематических ошибок (ошибок модели), существенно ухудшающих качество долгосрочного прогноза. Поэтому ниже «обучение» модели предлагается проводить в пространстве исходных переменных, что приводит к необходимости решения задач нелинейной регрессии. В связи с этим рассматривается эффективный метод численного поиска параметров нелинейных моделей, базирующийся на идеях генетических алгоритмов [37, 38].

Апробация предложенного способа оценки извлекаемых запасов (заключающегося в прогнозе динамики добычи нефти по модели С. П. Капицы, параметры которой определяются с помощью генетического алгоритма) показала, что он обладает рядом преимуществ по сравнению с традиционно применяемыми методами.

- = аV dt

(2.68)

где V - накопленная добыча нефти, t - время, - начальные извлекаемые запасы нефти = lim V , а - постоянная скорости роста.

V t J

Согласно (2.68) на начальном этапе развития нефтяного месторождения наблюдается экспоненциальный рост добычи нефти, а относительная скорость отбора нефти

= V dt

монотонно уменьшается, поскольку

dj = а dV

dt dt

< 0

(отметим, что если единицей измерения времени является год, то =Q-,

где Q - годовая добыча нефти).

Однако экспоненциальный рост и экспоненциальная асимптотика логистической кривой не удовлетворяют весьма существенному условию эволюции сложных природных систем - условию самоподобия (автомо-дельности) развития. Последнее может быть выражено в виде требования постоянства относительной скорости роста [36]

dVV.(Iz = а=const, (2.69)

V dt

где Г1 - некоторое опорное значение времени (точка автомодельности). Условию (2.69) удовлетворяет гиперболический рост по закону

V = C а, (2.70)

где C - постоянная интегрирования.

Легко видеть, что функция (2.70) удовлетворяет дифференциальным уравнениям

dV CVVY (2.71)

и d2а+г, (2.72)

dt (Г1 -1 )а+1 где C1 =аС--а, у=а, C2 =аС.

2.7.1. Эволюционные модели роста накопленной добычи нефти

В работе [35] динамику накопленной добычи нефти предлагается описать с помощью моделей, основанных на универсальном логистическом законе: