Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 [ 110 ] 111 112 113 114 115 116 117 118 119 120 121

кации на других участках месторождения следует вначале разбить скважины на две группы, используя координаты Парето, и проводить обработку только на скважинах второй группы.

in Qh

in r

Рис. 5.26. Зависимость логарифма дебита QH скважин от логарифма ранга r : о - до обработки (прямая 1); * - после обработки (прямая 2)

Одной из целей оптимизации разработки нефтяных месторождений является достижение однородности режимов работы скважин и выработки запасов нефти. Поэтому построение кривых Лоренца (см. раздел 5.4.1) в координатах «доля скважин» - «доля добычи» может оказаться весьма полезным инструментом для оценки неоднородности работы фонда скважин, а также для оценки изменения неоднородности после проведения тех или иных мероприятий. Количественные оценки могут быть получены путем вычисления значений коэффициента Лоренца (Джини).

Кривая Лоренца может быть использована также для оценки неоднородности строения пласта [33, 34]. Пусть ki, , (i = 1,2,...,N) - проницаемость, пористость и мощность i -го пропластка в разрезе пласта. Ранжируя пропластки в порядке убывания проницаемости, получим упорядоченную выборку k(i),m((),h)))}, с помощью которой вычислим частичные

суммы

>" N

и V =

Z m(()h(()

1=1

n = 1,2,..., N

Z m(k)h(() i=1

В случае однофазной фильтрации величина J имеет смысл доли

фильтрационного потока, притекающей к скважине через поры, занимающие долю v от общего объема пор, вскрытых данной скважиной.

Для примера, на рис. 5.27 приведена кривая Лоренца, характеризующая послойную неоднородность одного из участков пласта 4-6 Ма-монтовского месторождения.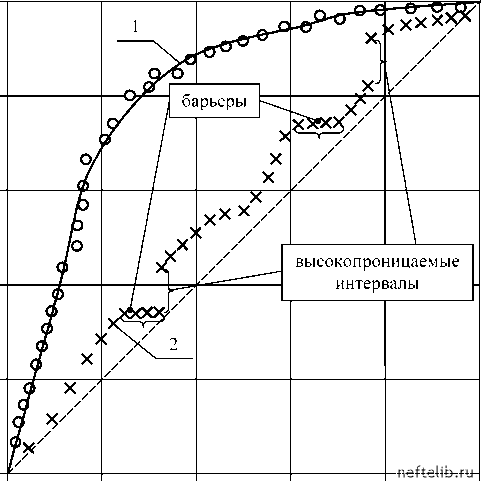

Рис. 6.27. Кривая Лоренца для неоднородного пласта 1 - Кривая Лоренца (L = 0,73); зависимость /И от V для статиграфически упорядоченных данных; О - ранжированные данные; X - неранжированные данные.

Как видим, 80% притока к скважине обеспечивается всего лишь 25% общей мощности пласта, что объясняется большой неоднородностью пласта (L = 0,73). На рис. 5.27 приведена также кривая /L = /ry) (кривая 2),

полученная для тех же данных, упорядоченных не по проницаемости, а стратиграфически (т. е. согласно глубине залегания). В работе [35] такие кривые предложено использовать для выделения так называемых «элементов потока» (flow units) - интервалов с более или менее однородными свойствами. Так, на кривой 2 хорошо видны высокопроницаемые интервалы и интервалы, образованные низкопроницаемыми породами (барьеры).

5.5. Нечеткие алгоритмы принятия решений

Как правило, принятие решений при управлении процессами разработки нефтяных месторождений (в частности, при определении желательности проведения или при оценке эффективности того или иного геолого-технического мероприятия) не может быть произведено с помощью одного единственного критерия (показателя эффективности). Так, при рассмотрении вопроса об остановке высокообводненных скважин следует принять во внимание не только величину обводненности продукции, но также гидродинамические последствия, связанные с перераспределением фильтрационных потоков воды и возможным «запечатыванием» запасов нефти. Еще один пример: анализ промысловых данных показывает, что эффективность ОПЗ скважин существенно зависит от большего числа геолого-геофизических (степень неоднородности пласта по разрезу, доля наиболее продуктивного прослоя в общей продуктивности) и промыслово-технологических (дебит нефти, обводненность продукции, темпы изменения дебитов нефти и жидкости) факторов, учет которых необходим при выборе скважин для проведения мероприятий.

Таким образом, типичной для задач контроля и управления процессами разработки месторождений является многокритериальность - наличие ряда показателей W1, W2, Wn, одни из которых желательно обратить

в максимум, другие - в минимум. Существенной особенностью многокритериальных задач является невозможность нахождения решения, одновременно удовлетворяющего всем критериям. Решение, обращающее в максимум один какой-то показатель, как правило, не обращает ни в максимум, ни в минимум другие. В такой ситуации математический анализ позволяет решить только ограниченную задачу «выбраковки» из множества возможных решений заведомо неудачных, уступающих другим по всем критериям решений. В результате отбрасывания заведомо непригодных решений образуется так называемое множество Парето - совокупность решений, характерных тем, что ни для одного из них не существует доминирующего

Подобные кривые могут оказаться очень полезными при обосновании необходимого числа слоев при создании трехмерных гидродинамических моделей.

Обратим внимание на то, что кривая 2 выглядит более изломанной, чем кривая 1, хотя они обе получены в результате интегрирования данных. Следовательно, ранжирование, используемое при построении кривой Лоренца, еще более «сглаживает» данные. В этом смысле операция ранжирования сама по себе подобна операции интегрирования. Это и понятно, поскольку при определении ранга единичного значения нужно «просмотреть» всю выборку.