Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 [ 116 ] 117 118 119 120 121

Случай а = 1 замечателен тем, что задача (5.69), (5.70) инвариантна относительно преобразований x -, ( - при всех значениях (0. Следовательно, эволюция системы в этом случае самоподобна (ср. с разделом 5.4). Зависимость (5.72) называется аллометрической и означает, что кривая x = x(t) может быть спрямлена в координатах in (- in x.

Развитие, происходящее в соответствии с аллометрической моделью, перекрывает существенно более длительные интервалы времени, чем развитие по экспоненциальному закону. Однако диапазон действия алломет-рической модели также ограничен, поэтому в координатах in (- in x кривая развития делится на ряд прямолинейных участков, переходы между которыми соответствуют критическим явлениям на более высоком иерархическом уровне системы.

Введя переменную ( = in (, уравнение (5.69) при а = 1 можно представить в виде

Для описания «сломов» аллометрической кривой нужно учесть зависимость параметра k0 от времени. Считая, что развитие на всех уровнях

иерархии идет подобным образом, получим

dx = k0

dp ~ T x,

откуда

in x = k0 in (+in c ,

т. е. кривая роста должна быть линейна в координатах in (- in in x.

Подставив (" = in ( и повторив всю цепочку рассуждений, можно получить модель еще более высокого уровня и т. д.

Описанные выше универсальные законы роста могут быть применены для анализа кривых накопленной добычи нефти VH (() при решении задач прогноза технологических показателей и выявления критических точек - моментов времени, соответствующих количественному изменению состояния разработки нефтяных месторождений.

На первом этапе разработки, соответствующем росту темпа отбора нефти за счет интенсивного разбуривания, кривая добычи описывается моделью

dV = k0 V

а на заключительной стадии, характеризующейся снижением темпов отбора, применима модель

dd;H = (X„0 - V„), (5.73)

от относительного числа скважин

v = n, n = 1,2,..., N,

qi - дебит i -й скважины (i = 1, 2,N), Q - суммарный дебит всех скважин,

Q = Z qi,

N - общее число скважин, участвующих в анализе.

где V„0 - начальные извлекаемые запасы нефти (предел VH при t ). Отметим, что уравнение (5.73) по виду совпадает с кинетическим уравнением Колмогорова, описывающем процессы кристаллизации металлов [43].

В качестве примера рассмотрим динамику добычи нефти и воды на месторождении Фортис (компания BP). Анализ кривой накопленной добычи нефти с использованием приведенных выше моделей показывает, что критические точки, соответствующие изменениям темпа отбора нефти и темпа обводнения, приходятся на 47, 73, 110, 163 месяцы разработки месторождения (см. рис. 5.31, 5.32). Отметим, что промежутки времени между двумя последовательными критическими точками (T1 = 26 мес.,

T2 = 37 мес. и T3 = 53 мес.) образуют геометрическую прогрессию со знаменателем

T2 = Т3 = 1,43,

что находится в соответствии с общей теорией критических уровней развития природных систем [41].

Одним из важнейших качественных показателей состояния разработки нефтяных месторождений является степень упорядоченности фильтрационных потоков. Для количественной оценки этого показателя могут быть использованы различные характеристики, позволяющие определить неравномерность распределения добычи нефти, газа и воды по добывающим и закачку воды по нагнетательным скважинам. В частности, весьма информативным показателем является коэффициент Лоренца (Джини), который в каждый данный момент времени вычисляется путем ранжирования (в порядке убывания) скважин по значениям дебитов нефти (газа) или воды или жидкости и построения зависимости накопленной доли суммарной добычи

Объем, млн. бар.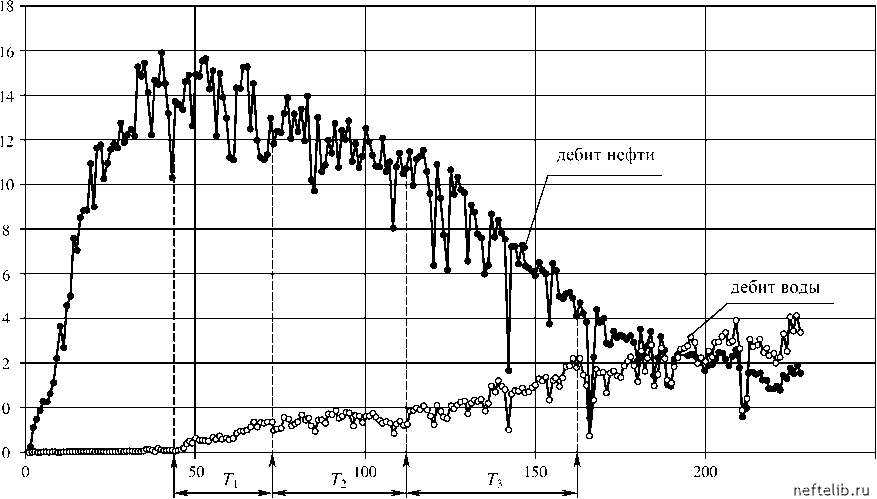

время, мес. 250

Рис. 5.31. Динамика отборов нефти и воды на месторождении Фортис