Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 [ 6 ] 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121

Ns (r )= r

где показатель Ds называется размерностью подобия.

Например, ковер Серпинского при к = 2 (см. рис 1.1) может быть покрыт тремя треугольниками, являющимися в 2 раза уменьшенными копиями исходного множества. Следовательно,

3 = 2Ds,

li 3

откуда Ds = log2 3 =--1,58.

Можно показать, что в данном случае размерность подобия совпадает с размерностью Хаусдорфа-Безиковича.

1.1.3. Реальные фракталы

Фрактальная самоподобность характерна для множества реальных систем. Она проявляется в геометрии деревьев и русел рек, строении легких, ветвлении кровеносных сосудов, динамике сердечных биений, изменении уровней водных поверхностей, турбулентности и т. д. Так, если рассматривать нейроны (нервные клетки) через микроскоп с небольшим увеличением, то можно отчетливо увидеть отходящие от тела клетки асимметричные разветвленные отростки (дендриты). При несколько большем увеличении можно наблюдать еще меньшие ответвления, отходящие от крупных ветвей. При еще большем увеличении обнаруживается новый уровень структуры: ответвления от ответвлений и т. д. (Тут можно вспомнить шуточное стихотворение «Если глянуть в микроскоп - там на клопе тоже клоп» [13].)

На каждом уровне масштаба структура ветвей нейрона подобна (хотя и не обязательно идентична, как в случае идеальных фракталов) структурам, наблюдаемым как в более крупных, так и в более мелких масштабах.

Можно показать, что траектория броуновской частицы, движущейся по плоскости, имеет размерность DH = 2, т. е. она практически полностью заполняет все двумерное пространство.

Заметим, что величину N(е) можно также определить как число кружков диаметром е , полностью покрывающих рассматриваемую кривую. При вычислении размерности DH может быть использовано покрытие кривой не кружками, а квадратиками с уменьшающейся стороной. В том случае, когда фрактальное множество вложено в трехмерное евклидово пространство, оно покрывается сферами или кубиками.

Существует ряд других определений размерности фрактальных множеств. Так, пусть NS (r) - число в r раз уменьшенных копий фрактала, необходимых для покрытия исходного множества. Тогда

Кипящая вода представляет собой фрактальную смесь паровой и жидкой фаз, в которой пузырьки пара содержат водяные капли, а каждая из этих капель - мелкие пузырьки газа, которые, в свою очередь, содержат еще более мелкие капли воды, и т. д. [14].

Отличие реальных фракталов от идеальных заключается в том, что первые обладают характерным минимальным линейным размером (например, таким как радиус атома или молекулы), в то время как идеальные фракталы имеют бесконечно тонкую структуру. На практике существует и характерный максимальный размер фрактала (так называемый радиус корреляции). Реальная среда как бы составлена из фрактальных блоков размерами и поэтому на масштабах, больших , может считаться обычным (евклидовым) объектом.

Образование фрактальных структур в природе происходит за счет таких механизмов, как кластерообразование при агрегации отдельных частиц, осадкообразование, развитие неустойчивости поверхности раздела при вытеснении из пористой среды одной жидкости другой, перемешивание жидкостей, растрескивание материалов, пробой диэлектриков и т. д.

Фрактальные размерности реальных объектов можно определить путем покрытия их фотографий квадратиками £Х£ и нахождением связи между числом квадратов N(е) и длиной сторон квадратов £. Согласно (1.2)

lnN(е) = lnC- Dh lne. (1.3)

Поэтому в координатах (lne, ln N(е)) должна получиться прямая

линия, по угловому коэффициенту которой определяется величина Вн. Если точки не лежат на одной прямой, то изучаемый объект

нельзя признать фрактальным.

Следуя [13], можно утверждать, что реальные фрактальные структуры представляют собой след хаотических процессов. Где бы в природе в результате хаотического процесса ни формировался тот или иной объект (берег моря, атмосфера, геологический разлом и т. д.), повсюду с большой вероятностью можно обнаружить фракталы (в контуре береговой линии, в форме облаков, в конфигурации скальных образований).

Повсеместная распространенность фракталов во многом объясняется тем, что они могут быть получены наложением двух простейших преобразований - растяжения и наложения, часто встречающихся в природе. Проиллюстрируем это (не очень строгое) утверждение на примере преобразования подковы (рис 1.5, а-в), итерации которого приводят (рис 1.5, г, д) к образованию фрактальной структуры [15].

Аналогичные преобразования имеют место при перемешивании жидкостей, когда имеют место периодически повторяющиеся вытягивания и изгибы участков жидкостей с возвращением их в исходное положение. Поэтому если в сосуд с краской капнуть несколько капель краски другого

цвета и начать перемешивать, то через некоторое время капли растянутся в тонкие слои, образующие фрактальную структуру [16, 17]. Получаемая при этом картина удивительно похожа на узоры, встречающиеся иногда на поверхности камней, подобранных на берегу. Возможно, эти породы образовались при застывании смеси, полученной перемешиванием расплавов минералов различного цвета.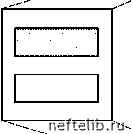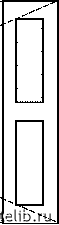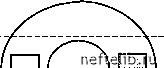

Рис. 1.5. Преобразование подковы

Много фракталоподобных образований содержится в человеческом организме [18]. Они играют важную роль в поддержании нормального функционирования организма. Так, фракталоподобная структура артерий и вен осуществляет равномерное кровоснабжение разных участков органов, фрактальные ответвления и складки значительно увеличивают поверхность всасывания в кишечнике, способствуют распределению, сбору различных веществ (в кровеносных сосудах, желчных протоках и бронхиалах) и информации (в нервной системе).

Последовательные изломы, изгибы и ветвления позволяют линейной структуре (кривой Коха, например) «почти» заполнить пространство. Точно таким же образом линейная система артерий почти сплошь пронизывает трехмерный организм, обеспечивая его бесперебойное кровоснабжение.

Образно говоря, здесь фрактал выступает как способ организовать взаимодействие пространств различной размерности [13].