Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 [ 22 ] 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121

Таким образом, величина w (s,т) характеризует плотность энергии в

пространстве (т, s).

Поскольку сжатие вейвлета приводит к увеличению частоты его ос-цилляций, то разложение по вейвлетам подобно оконному преобразованию Фурье с шириной окна, уменьшающейся при увеличении частоты гармоники (см. рис. 1.22, в). Изменчивость частотно-временного окна позволяет вейвлет-анализу одинаково хорошо выявлять и низкочастотные, и высокочастотные характеристики сигналов, т. е. «увидеть и лес, и деревья» [42].

Диагностирование с помощью вейвлетов

Из сказанного выше ясно, что вейвлет-анализ колебаний («шумов»), зарегистрированных в ходе нормальной эксплуатации объектов управления, может стать эффективным инструментом диагностики. Преимуществом этого метода перед анализом Фурье является адекватность изменчивой, разномасштабной структуре реальных сигналов.

Вейвлет-представление позволяет:

- локализовать особые точки;

- проанализировать частотную и амплитудную изменчивость сигнала;

- выявить нерегулярные выбросы функции и её производных;

- вычислить фрактальные характеристики сигнала.

В качестве одной из иллюстраций возможностей метода рассмотрим вейвлет-преобразование двух модельных сигналов (см. рис. 1.21) с помощью материнского вейвлета МНАТ.

В верхней части рис. 1.23 приведены распределения значений коэффициентов разложения w(s,т) (по горизонтали - переменная т, по вертикали - ось S в логарифмическом масштабе, светлые тона соответствуют большим значениям коэффициентов w ). Как видим, МНАТ-преобразова-ние позволяет четко различить два сигнала и обнаружить момент разладки для второго сигнала.

Рис. 1.23. Результат вейвлет-преобразования (МНАТ) для модельных сигналов

В ряде случаев вейвлет-представление можно рассматривать как формализацию приемов анализа временных рядов, разработанных ранее, исходя из других позиций. Так, существует глубокая связь между методами обнаружения системы состояния по изменению производной сигнала [43] и вейвлет-анализом. Для иллюстрации этого рассмотрим МНАТ-преобразование функции с особенностью - разрывом производной (рис. 1.24). Вейвлет-преобразование (верхняя часть рис. 1.24) точно указывает на расположение особенности [41].

Эту точку можно было бы обнаружить и напрямую, путем численного дифференцирования временного ряда. Однако, как известно, дифференцирование экспериментальных данных является некорректной операцией из-за неустойчивости относительно ошибок замеров (см. [44], а также раздел 2.1.3). Поэтому диагностирование по производной при наличии «шумов» затруднительно. А вот вейвлет-преобразование, как показывают расчеты, дает устойчивые результаты даже при достаточно большой «зашумленности» данных. Регуляризующие алгоритмы вычисления производных связаны с удалением шумов и перемасштабированием, что и делает вейв-лет- преобразование. Таким образом, вейвлет-анализ обладает регуляри-зующими свойствами.

Рис. 1.24. Вейвлет-преобразование функции с разрывом производной

Пример диагностирования состояния оборудования с помощью вейвлет-анализа

В заключение рассмотрим конкретный пример использования вейв-лет- анализа для диагностирования состояния бурильного долота по измерениям случайных колебаний давления промывочной жидкости P{t )и осевой нагрузки на долото G{t ), произведенным в ходе бурения скважины.

На рис. 1.25 приведены результаты вейвлет-анализа колебаний осевой нагрузки G{t ) в начале (а) и конце (б) работы долота, которое после подъема на поверхность оказалось практически неизношенным. На рис. 1.25, а (новое долото) различаются многочисленные периодически по-

вторяющиеся детали в верхней части, что соответствует низкочастотным модам. Для рис. 1.25, б (незначительно поврежденное долото) характерно появление высокочастотных составляющих в нижней части картины.

На рис. 1.26 представлено вейвлет-преобразование колебаний G(t) в начале и конце работы долота, которое после подъема оказалось сильно изношенным.

В низкочастотной области на протяжении всего интервала масштабы деталей сохраняются, прослеживается похожая на периодическую структура. Когда долото изношено (рис. 1.26, б), в высокочастотной области появляется большое количество мелкомасштабных деталей, что говорит о наличии хаотических колебаний долота, вызванных его повреждениями.

Расчеты показали, что для параллельной количественной оценки технического состояния долота могут быть использованы величины:

где E (G ) и E (P) - полная энергия колебаний давления промывочной жидкости и осевой нагрузки, верхние индексы H и K обозначают начало и конец работы одним долотом. (Отметим, что пределы интегрирования при вычислении энергии в начале и в конце долбления должны быть одинаковыми.)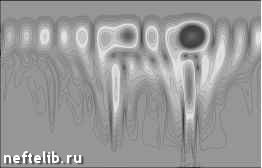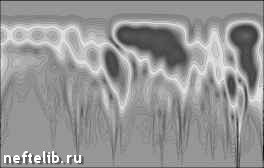

Рис. 1.25. Масштабно-временная развертка для неизношенного долота в начале и в конце интервала бурения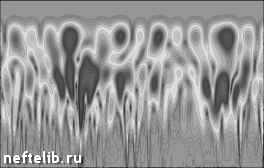

Рис. 1.26. Масштабно-временная развертка для изношенного долота в начале и в конце интервала бурения