Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 [ 93 ] 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121

0,15 -

0,10 -

0,05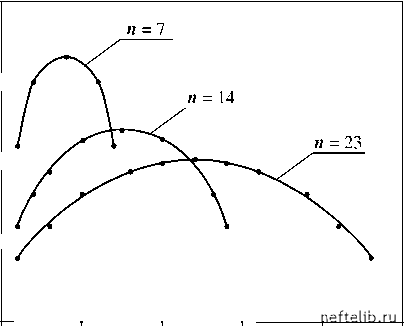

Рис. 5.1. Зависимость относительного отклонения порядковых статистик от ранга

Нетрудно видеть, что секрет успеха - в априорной информации, а именно в информации о законе распределения генеральной совокупности. Без знания функции распределения, конечно, ничего подобного сделать нельзя.

Мощным источником дополнительной информации является также операция ранжирования. Это можно показать количественно, оценив изменение энтропии в ходе упорядочивания. Поскольку число различных реализаций выборки равно n! и все реализации равновероятны, то энтропия выборки до ранжирования равна [1]

H =- In

In n!.

Упорядоченная же выборка может быть реализована только одним способом, т. е. ее энтропия равна нулю. Как известно, уменьшение энтропии является мерой информации, поступившей в систему. Следовательно, процесс ранжирования приводит к «накачке» выборки информацией в объеме In n!.

Знание законов распределения немногое может дать наблюдателю, снабженному измерительным прибором: с его помощью можно лишь несколько улучшить измерительную процедуру. Как мы видим, качественно иная ситуация возникает, когда измерительного прибора нет. В этом случае знание закона распределения позволяет восстановить отсутствующую информацию. В первом приближении в качестве оценки любого значения величины X можно выбрать среднее по генеральной выборке E(X ), но

эта оценка слишком грубая. Если же имеется компаратор, то можно организовать достаточно точное измерение с помощью упорядоченных выборок большого объема. В этом случае n величин «помогают» друг другу «измерить» самих себя.

5.1.2. Практическая реализация расчетов

При практическом применении описанных выше алгоритмов необходимо решить задачу определения математических ожиданий порядковых статистик Er (r = 1,2,..., n) при известной функции распределения. Для

этого можно воспользоваться готовыми статистическими таблицами, в которых приведены значения Er при разных значениях n для ряда

наиболее часто встречающихся функций распределения. Отметим, что эти

таблицы составлены для нормированных распределений (равномерного

распределения с a = 0, b = 1, нормального закона с E = 0, а = 1 и т. д.).

Поэтому при их применении необходимо осуществить преобразование к

нормированным случайным величинам:

~ x - a

x =-

b - a

для равномерного распределения и

~ x - E

x =-

для нормального закона.

При достаточно больших объемах выборок можно использовать приближенную формулу [1, 4, 5]

F (Er ) = .

n -1

Обращая функцию распределения, получим

f r -1

Er =Ф -1 , (5.2)

где Ф(z F-1 (z).

Часто информация о законе распределения случайной величины является неполной - мы знаем вид функции распределения, но не знаем значений параметров этой функции (например, математического ожидания и дисперсии). В этой ситуации оказывается необходимым все же сделать несколько прямых замеров с помощью эталонов.

Пусть, например, известно, что величина x распределена по некоторому двухпараметрическому закону, значения параметров которого однозначно связаны с математическим ожиданием E и дисперсией а2. Предположим также, что в нашем распоряжении имеются таблицы математических ожиданий порядковых статистик Er, составленные для нормализо-

~r1 r1 (5.4)

E + oEr = x(r ),

где x(r ), x(r ) - измеренные значения случайной величины.

Решив (5.4) относительно E и о , можно оценить и значения остальных элементов упорядоченной выборки:

x(r) = E + oEr (r = 1,2,...; n, i Ф Г2 ).

Надежность оценок E и о может быть повышена, если удается сделать более чем два прямых замера. При этом мы имеем переопределенную систему уравнений

E + oEr = x(r), k = 1,2,...,m < n,

которую необходимо решать методом наименьших квадратов.

Описанная процедура оценок полезна в тех случаях, когда измерения с помощью эталонов можно организовать только для некоторых членов выборки или когда замеры слишком дороги. Так, вновь возвращаясь к задаче об измерении веса камней, предположим, что мы знаем: они распределены по равномерному закону, но параметры распределения a и b неизвестны. Гирь у нас нет, но они есть у меркантильного соседа, который за каждый замер с помощью его гирь требует 100 долларов. Для прямого измерения веса 1000 камней нам понадобилось бы 100 тысяч долларов. Если же привлечь алгоритмы порядковых статистик, то можно ограничиться взвешиванием (всего лишь за 200 долларов) двух камней x(r1) и x(r2) в ранжированной выборке, определить a и b из системы

a + (b - a ) = x(),

n +1 1 (5.5)

= x(

a + (b - a)-= x(r )

n + 1 r2

ванной функции распределения заданного вида (т. е. для функции с E = 0 и G = 1). Математические ожидания ненормализованных величин определяются с помощью табличных значений Er по очевидной формуле

= E + GE~r., r = 1,2, n. (5.3)

Для определения неизвестных значений E и о необходимо напрямую измерить значения двух реализаций величины X . Если в выборке объемом n эти измеряемые значения имеют ранги r1 и r2 , то E и о могут быть найдены из условий

Er1 = x(r1), Er2 = x(r2),

что, с учетом (5.3), приводит к системе