Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 [ 96 ] 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121

Предположим, что мы измерили n значений yi при различных (неизмеренных) значениях xi. Отранжировав выборку {yi}, мы, тем самым, отранжируем и выборку {xi} (не теряя общности, можно считать функцию (p(x) монотонно неубывающей). В соответствии с алгоритмом безэталонных измерений мы можем теперь вместо неизвестных ранжированных

значений x(r) взять их оценку через порядковые средние x(r) = Er и идентифицировать зависимость y = p(x) по связи между y(r) и x(r). В этом и

состоит идея безэталонной идентификации.

Отметим, что после ранжирования наблюдения становятся коррелированными, в то время как классический метод наименьших квадратов требует некоррелированности данных. Поэтому при безэталонной идентификации рекомендуется использовать обобщенный метод наименьших квадратов [1, 2].

Если известен только вид функции распределения x, то параметры ее могут быть определены путем прямого измерения некоторых реализаций x, как это описывалось выше.

Пример 4. Математический эксперимент по восстановлению линейной зависимости

вале

Пусть \0;1

случайная величина, равномерно распределенная в интер-y - переменная, связанная с ней функциональной зависимостью y = 2 x + 1. Воспользовавшись генератором случайных чисел, образуем выборку {xi } (i = 1, 2, ...,10)случайных реализаций x и связанную с ней выборку «наблюдений» {yi}, где yi = 2 xi +1, после чего произведем ранжирование по величине y (см. табл. 5.2).

Таблица 5.2

Исходные данные для математического эксперимента

Предположим теперь, что сами значения x(r) каким-то образом утеряны, сохранилась лишь информация о том, что x - равномерно распределенная случайная величина из интервала [0; 1]. Тогда упорядоченным значениям y(r ) можно поставить в соответствие оценки

x (r ) = Er =-, n = 10

n +1

построить зависимость y(r) от x(r) (см. табл. 5.2 и рис. 5.4, где точ-

x (r), y(r) представлены черными кружками).

y(r)

0 0,2 0,4 0,6 0,8

Рис. 5.4. Зависимость y(r) от x(r).

По расположению точек видно, что зависимость между y(r) и x(r) можно искать в виде линейной функции

y(r ) = а x (r)+ b.

Используя стандартный метод наименьших квадратов, получим a = 2,36, b = 0,80 (прямая 1 на рис 5.4).

Качество идентификации (напомним, что точные значения параметров a = 2, b =1) может быть улучшено, если для определения a и b ис-

пользовать только крайние статистики (как уже отмечалось, в случае равномерного закона распределения наиболее информативны именно они). Тогда легко получить

2,1,

y(n) - y(1) л л x (n)-x(1)

x(n) y(1)- y(n)= 1,0

(6.7)

x(n)- x(1 )

(прямая 2 на рис. 5.4). Эти значения параметров очень близки к точным.

Отметим, что соотношения (5.7) могут быть получены и другим путем, а именно при применении обобщенного метода наименьших квадратов, разработанного, как мы уже отмечали, для коррелированных данных [1].

Q, м3/сут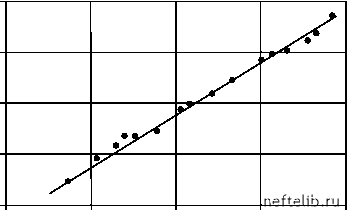

700 Угр, М3/Сут

Рис. 5.5. Зависимость дебита нефти от расхода газа

Пример 5. Безэталонная идентификация характеристики газлифтной скважины

Результаты расчетов, проведенных выше в примере 1, позволяют провести безэталонную идентификацию рабочей характеристики газлифт-ной скважины, т. е. определить зависимость Q = QV). Для этого построим (см. рис. 5.5) зависимость между дебитом нефти Q и расчетным расходом газа (второй и шестой столбцы табл. 5.1). Аппроксимируя эту зависимость (в рассматриваемом диапазоне изменения ) прямой, получим

Q = 2,0Ю-2V, -5,4.