
 |
|
|
Главная Переработка нефти и газа т. е. кроме точки P имеется еще одна точка равновесия - начало координат O . Построив ломаную траекторию, выходящую из любой близкой к O точки, можно показать, что эта точка равновесия является неустойчивой: малейшее смещение вправо от O приводит к быстрому росту величины этого смещения. Рассмотрим типы движений, возникающих при различных значениях параметра /и. 1. 0 < и< 1. Система имеет только одно положение равновесия x*= 0, и оно устойчиво. Так, если /1 = 0,5 и x0 = 0,8, то x1 = 0,08, x2 = 0,0368, x3 = 0,0177, ... 2. 1 < и< 3. При и = 1 происходит бифуркация, в результате которой точка равновесия x* = 0 теряет устойчивость и появляется новый аттрактор x*2 = 1 - -. Так, если / = 2 (x*2 = 0,5) и x0 = 0,1, то x1 = 0,18, x2 = 0,2952, x3 = 0,4161, x4 = 0,4859, x5 = 0,4996, ... 3. 3 < и< 1 V6 ~ 3,45 . При /и = /1 = 3 точка равновесия x*2 становится неустойчивой и вместо нее появляется устойчивый предельный цикл, соответствующий колебаниям с периодом 2 (рис. 1.15, а). 4.1 V6 < и< /и„ = 3,5699. При /и = /2 = 1 л/б двукратный цикл сменяется четырехкратным (см. рис. 1.15, б), который, в свою очередь, при и = /3 ~ 3,54 сменяется циклом периода 8, и т. д. Таким образом, за счет последовательного удвоения периода, движение постепенно усложняется до тех пор, пока при значении ~ 3,56994 не произойдет переход к хаосу (см. рис. 1.15, в). Величина является точкой сгущения последовательности бифуркационных значений /1, /2, ... , , ... , причем, начиная с некоторого n, выполняется асимптотический закон Фейгенбаума [24] =и--C, (1.14) где о = 4,66920 - число Фейгенбаума. Закон (1.14) имеет универсальный характер, поскольку он проявляется во многих численных и физических экспериментах в системах самой различной природы. Можно утверждать, что переход к хаосу путем последовательного удвоения периода движения, подчиняющийся закону (1.14), является одним из универсальных сценариев возникновения случайных движений в детерминированных системах. Другие возможные пути перехода к хаосу широко обсуждаются в специальной литературе [4, 5, 15, 20, 21]. xn А :z5xzwxzi":: xn A 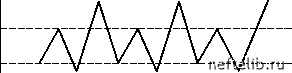 xn A 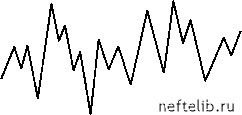 Рис. 1.15. Усложнение движения по логистическому закону 1.3. Репликации иелииейиой динамики Согласно Г. Хакену [2, 25] синергетику следует рассматривать как наиболее разработанную теорию самоорганизации, которая может быть применена к широкому кругу разнообразных явлений в сложных системах самой различной природы. В этом качестве синергетика уже стала социо- культурным феноменом, оказавшим мощное влияние на все науки, изучающие сложные природные объекты. Всем им свойственна эмержент-ность (от англ. emerge - «появляться»), т. е. наличие интегративных свойств, не выводимых из известных свойств элементов и способов их соединения. Взаимодействие микроскопических элементов приводит к появлению на макроскопическом уровне качественно новых свойств и особенностей. Цель синергетики состоит в том, чтобы соединить эти два уровня -микро- и макроскопический. Она показала, что в большинстве случаев новые структуры создаются не некоей организующей рукой, а самими системами. Под влиянием внешних потоков энергии и вещества структурные модули, составляющие сложные системы, взаимодействуют друг с другом нелинейным образом, хаотично «пробуя» различные формы коллективного поведения. По мере возрастания интенсивности внешних потоков система подходит к точке выбора (бифуркации), после которой начинает преобладать некоторый выделенный тип кооперативного поведения. Синергетика предложила также способы «сжатия» огромного количества информации, которую необходимо было бы обработать при описании системы как совокупности ее отдельных частей. Такое «сжатие» возможно, поскольку изменения системы в макроскопических масштабах управляются параметрами порядка, число которых невелико (принцип подчинения). В определенном смысле параметры порядка действуют как кукловоды, заставляющие кукол плясать [25]. Известным физическим примером, иллюстрирующим этот принцип, является кювета с жидкостью, подогреваемой снизу. Параметром порядка здесь является разность температур между нижней и верхней поверхностями жидкости. Как показывают опыты, когда разность температур превышает некоторое критическое значение, внезапно становится видимым макроскопическое конвективное движение жидкости, порождающее ячеистую структуру наподобие пчелиных сот (ячейки Бенара, см. рис. 1.16). Здесь изменением одного параметра удается организовать управление движением огромного количества молекул, подверженных хаотическому тепловому движению. Примером аналогичной бифуркации в коллективном поведении сообщества людей является появление единого ритма в аплодисментах зрителей по окончании всем понравившегося концерта: эти аплодисменты переходят в единодушные ритмические хлопки, когда управляющий параметр системы (энтузиазм аудитории) превосходит некоторый порог [14]. Следует, однако, отметить, что в последнем примере управляющий параметр не задается извне (как температура подогрева жидкости в кювете), а вырабатывается самой системой. В системах живой природы (в отличие от физических систем) управляющие параметры в определенном 0 1 2 3 4 5 6 7 8 9 10 11 12 [ 13 ] 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 |
||
 |
 |