Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 [ 87 ] 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121

еще одно равновесное значение уравнения

точка 01(л10, л20), где n

решение

1 + n1s0 +110

= 1 +

1 + ns

n20 = n10

1 + ns

10 v

При малых величиной An10 можно пренебречь. При этом

=(r - 1)). (4.14)

Используя метод D-разбиений [12], построим области устойчивости стационарных решений.

Для нулевого решения получим характеристическое уравнение

£р 2 +(£ + 1)р +1 + (а£ р - r )e~рт = 0. (4.15)

Произведем D-разбиение в плоскости (а- r). Подставив в (4.15) р =ia, получим

aecosinwr - r cosaT = eaP - 1,

aecocoswT + r sinaT = -(e + 1)a.

Определитель этой системы А = £а. Следовательно, границы D-областей

определяются особой прямой r =1 и кривой, параметрическое уравнение которой имеет вид

а =-ta2 - 1 sin ат - (£ + 1)acos ат ,

£ (4.16)

r = - (i£ + 1)аsinат +(fa2 - 1)cosат . Соответствующее D-разбиение представлено на рис. 4.21, заштрихованная область есть область устойчивости D(0). В параметрической форме

дуга АВС определяется уравнениями (4.16) при 0 <a<a1, где a1 -наименьший положительный корень уравнения

(f + l)asinaт+(£•a2 - l)cosaт = -1. Из рис. 4.21 ясно, что система устойчива при

а1 <а<а2; < r < 1, где а1 = lim а = -(т + £ +1).

0 £

а2 = aa1), = (а1, £, т), (а, £, т) - уравнение дуги АВС. При r > 1 система апериодически неустойчива, а при r < r* - периодически неустойчива. Из приведенного выше анализа следует, что для всех а, £, т при r > 1 точка равновесия О (0, 0) теряет устойчивость (здесь не рассматривается периодическая неустойчивость стационарного решения О (0, 0), поскольку величины n1 и n2 могут принимать только положительные значения). При этом у системы (4.13) появляется новое положение равновесия О (n10, n20). Исследуем устойчивость этой точки.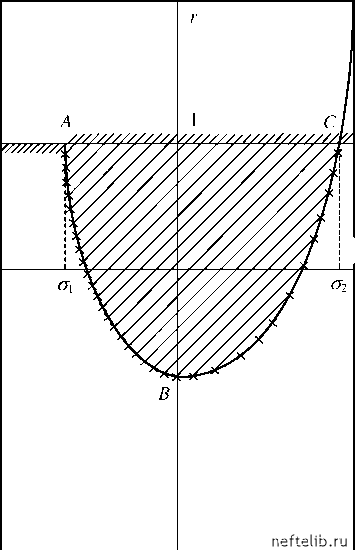

Рис. 4.21. D-разбиение

Соответствующее характеристическое уравнение получается из (4.15) заменой £ на 0 = (1 - П20 )2, g на g0 = g f, r на

Г0 = М - П20)2 -G\f ,

1 + (1 - S )n1S0

1 + n10

Для простоты рассмотрим случай малых м, когда n10 определяется выражением (4.14) и 1 - n20 ~ 1. При этом

£0 = £, G0

Ь - 1)(r - 1)-1

(s - Hr - 1) - 1

Из рис. 4.21 следует, что если а0 <а1, а0 > а2 или Г0 < rm, где rm =(0,£,т), то стационарное решение (n10, n20) неустойчиво. При а1 < а < а2 точка равновесия O1 устойчива, если Г0 >(а0,£,т), и периодически неустойчива, если Г0 < (а0,£,т).

Численные расчеты показывают, что при переходе через границу периодической неустойчивости, вследствие увеличения значения r, вначале возникают периодические колебания n1 (t), n2(t), а затем через каскад бифуркаций удвоения периода - хаотические колебания.

Поскольку, как легко видеть,

( а , r = а--1

ldG0

то при постоянных а, а и д все эти бифуркации связаны с уменьшением G0 - расхода в отсутствие зародышей. Поэтому при проведении расчетов фиксировались значения величин v, а, A1 =- и варьировался пара-

£

метр b = - = -G0. Оказалось, что при уменьшении расхода после потери £ у

устойчивости точки равновесия O1 вначале возникают периодические колебания величин n1, n2, а затем через каскад бифуркаций удвоения периода - хаотические колебания. Так, численное интегрирование (4.13) при т= 5, N = 5, v = 20, а = 0,5, A1 = 1 показало, что при b = b0 ~ 8,2 происходит переход от точки равновесия О1 к предельному циклу. В точках b1 ~ 6,5, b2 ~ 5,58, b3 ~ 5,38 происходят бифуркации удвоения периода, которые завершаются переходом к хаотическому движению в точке сгущения b = b0 ~ 5,31. Для примера на рис. 4.22 представлена зависимость G = G(t), соответствующая хаотическим колебаниям, возникающим при b = 5,25.

Из полученных выше результатов следует, что при достаточно больших значениях G0 накопления зародышей на стенках не происходит. При уменьшении расхода система переходит в новое стационарное состояние, характеризующееся большим значением пропускной способности трубки. Дальнейшее уменьшение расхода приводит к возникновению вначале периодических, а затем хаотических колебаний пропускной способности. Эти выводы находятся в согласии с приведенными выше экспериментальными данными.

Расчеты показывают, что периоды автоколебаний порядка т. Поскольку характерные времена изменения пропускной способности трубы составляют 30-60 мин (см. рис. 4.20), то такой же порядок должно иметь время роста зародышей. Характерное время диффузионного прито-