Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 [ 98 ] 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121

На рис. 5.6 зависимости (5.14)-(5.17) представлены кривыми 1-4 соответственно. Как видим, зависимость (5.7) хорошо описывает экспериментальные результаты Кригера [9], представленные на рисунке черными кружками.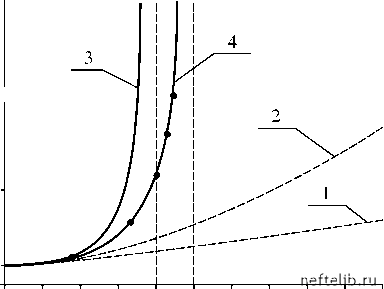

Рис. 5.6. Зависимость вязкости суспензии от концентрации твердых частиц • - экспериментальные точки; 1-4 - расчетные кривые.

Этот красивый пример, приведенный в [8], наглядно показывает, как априорная информация (в данном случае информация об особенности функции) позволяет восстановить вид зависимости, опираясь на сведения о ее поведении в «малом».

5.2.3. Приток к несовершенной скважине

Скважина, вскрывающая пласт толщиной h только частично (см. рис. 5.7), называется несовершенной по характеру вскрытия. Для расчета радиального притока к такой скважине удобно использовать обобщение формулы Дюпюи в форме

2 п kh (Pk - Рс)

In Rk + S

(5.18)

где Q - дебит скважины, k - проницаемость в горизонтальном направлении, и 0 - вязкость и объемный фактор жидкости, RK - радиус контура питания, rc - радиус скважины, PK - давление на контуре питания, Pc -давление на забое скважины, S - скин-фактор.

"И

1. -

Рис. 5.7. Несовершенная по стенени вскрытия скважина

Величина S характеризует уменьшение дебита скважины из-за неполного вскрытия и зависит [10] от двух безразмерных величин

S = h

вертикальная проницаемость

где a - толщина вскрытой части пласта, k1 пласта.

Вообще говоря, зависимость S = S (/г,) должна быть определена из

решения фильтрационной задачи о радиальном притоке к несовершенной скважине, но в точной постановке эту задачу решить сложно.

Приближенное решение легко получить методом Паде-аппроксима-ции. При построении аппроксиманта учтем естественное требование

S -oo (q 0) при ~ 0, а также поведение функции S = S (h,s) в малой окрестности точки h =1.

Разложение решения вблизи h =1, полученное асимптотическими методами, имеет вид (подробности расчетов не приводим)

S = (a + 4,60) z + (A - 7,29) z2 +(A + 50,34) z3 +(5.19)

где z = 1 - h, a = ln(4S).

С учетом априорного требования S при h 0 (z 1) будем искать Паде-аппроксимацию в виде

az+вz2

1 -(1 + r)z + 7

(5.20)

In rk + S (h,S)

от степени вскрытия пласта h , полученные с учетом формулы (5.21)

для = 1250 при S = 100 (кривая 1) и S = 1000 (кривая 2). Для сравнения

здесь же приведены данные В. И. Щурова, полученные на электрон-аналоговых моделях (кружки), и результаты численного расчета из работы [11]

(квадратики) для тех же значений - и S.

Как видим, во всей области изменения h , представляющей интерес (hi > 0,1), мы имеем хорошее совпадение результатов. Кривые 1 и 2 на рис 5.8 представляют собой графики разложений (5.19) и приведены для иллюстрации того, насколько эффективен переход к Паде-аппроксиман-там.

5.2.4. Построение корреляцией для остаточной нефтенасыщенности и коэффициента вытеснения

Одной из основных физико-химических характеристик нефтяного пласта является коэффициент вытеснения нефти водой

в = shh - sho shh

где shh и sho - начальная и остаточная нефтенасыщенность.

Разложив (5.20) в ряд в окрестности z = 0 и приравняв коэффициенты при одинаковых степенях z в (5.19) и (5.20), получим систему

а = A - 4,60, < в-а(1 -г)= A + 7,9,

(1 + у)(сх + в) + аг = A - 50,3, решение которой имеет вид

а = A - 4,6, < в = 4,85 A -10,4, 7 =-4,85. Таким образом, окончательно получим

S = (A - 4,6) - ~)+ (4,85 A -10,5) - /~ )2 . (521)

1 -(1 + 4,85) - ~)+ 4,85 (1 - ~ )2 На рис. 5.8 приведены зависимости коэффициента гидродинамического совершенства скважины

In Rk

П= c