Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 [ 20 ] 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121

м3/сут

I 250

Рис. 1.20. Замеры дебита жидкости

1 - эффективная ветвь регулировочной кривой, 2 - неэффективная (нисходящая) ветвь.

В табл. 1.1 приведены значения показателя Херста, вычисленные по временным рядам замеров дебита жидкости, снятых на нескольких газ-лифтных скважинах этого же месторождения при работе в двух различных режимах. Как видим, при переходе на неэффективную ветвь значение H уменьшается. Обращает на себя внимание тот факт, что работа в оптимальном режиме характеризуется значениями H, принадлежащими области 0,7<H<0,8, в которой чаще всего и располагаются показатели Херста природных процессов [6, 9].

Таблица 1.1

Значения показателя Херста

Таким образом, показатель Херста может быть использован для диагностирования режима работы газлифтной скважины по данным нор-

1.4.3. Вейвлет-анализ в задачах диагностирования

Соображения о фрактальном характере природных объектов позволяют объяснить повышенное внимание к сравнительно новому методу обработки временных рядов замеров - вейвлет-анализу [40-42]. Этот метод заключается в разложении исходного сигнала по базисным функциям, полученным из некоторого прототипа (mother wavelet) путем сжатий, растяжений и сдвигов по времени. Английский термин «wavelet» означает «маленькая волна» или «всплеск». Этим названием подчеркивается то обстоятельство, что вейвлеты быстро спадают до нуля за пределами некоторого конечного интервала в отличие, например, от бесконечно осциллирующих синусоид, по которым сигнал раскладывается в рамках традиционного анализа Фурье. Компактность вейвлетов позволяет осуществить локальный анализ сигналов и проследить изменчивость их частотно-масштабных характеристик.

Поэтому основные приложения вейвлет-анализа заключаются в локализации особых точек (точек разладки) и проведении частотно-временного анализа сигналов. Из описания способа построения вейвлетов ясно, что они должны быть идеальным инструментом для раскрытия масштабно-инвариантных (фрактальных) свойств временных рядов. Если добавить, что вейвлет-анализ хорошо приспособлен к анализу нестационарных сигналов, то станет ясно, что он может стать мощной альтернативой преобразованию Фурье.

Вейвлет-анализ нашел широкое применение при диагностировании состояний объектов управления, поскольку его использование позволяет адекватным образом исследовать масшабно-инвариантную динамику сложных технических систем. Преимуществом вейвлет-анализа также является возможность локальной оценки разномасштабных частотных характеристик временных рядов, что особенно ценно при решении задач распознавания разладок.

мальной эксплуатации (т. е. при работе на одном фиксированном режиме закачки газа). Это позволяет избежать затрат, связанных с проведением активных экспериментов по экспериментальному определению зависимости Q = Q(V) (см. выше). При первом взгляде на рис. 1.20 может показаться, что в качестве диагностического признака можно использовать и более привычные статистические характеристики (относительное квадратичное отклонение, например). Однако анализ показывает, что величина показателя Херста является более информативным признаком. Кроме того, мы предполагаем, что фрактальные характеристики будут не заменять собой другие более известные признаки, а использоваться наряду с ними для повышения надежности принимаемых с их помощью решений.

Ниже описана методология вейвлет-анализа и приведены примеры его использования в задачах диагностики.

Вейвлет-преобразование

Многие трудности, возникающие при анализе процессов с помощью преобразования Фурье, связаны с тем, что «архитектура» реальных сигналов не может быть адекватным образом описана с помощью бесконечных гармоник.

Как правило, регистрируемые сигналы нестационарны, их частотные и масштабные характеристики со временем меняются, причем очень важно локализовать моменты, соответствующие изменению этих характеристик (моменты разладок), поскольку они, как правило, связаны с изменением состояния объектов управления.

Преобразование Фурье не позволяет решать задачу локализации. Например, оно не отличает сигнал, представляющий собой сумму двух синусоид с разными частотами, от сигнала, состоящего из тех же синусоид, включающихся одна за другой [40] (см. рис. 1.21).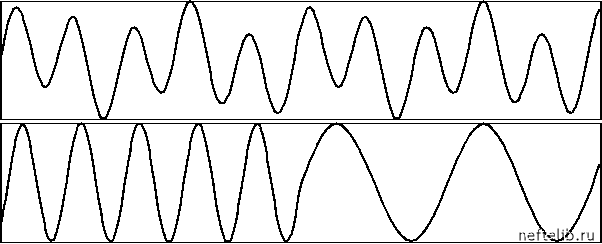

Рис. 1.21. Два сигнала с подобными Фурье-спектрами

Частично эта трудность снимается за счет использования оконного преобразования Фурье

F(a, т)= If (t)g(At,t -т)ехр(- iat)dt,

где f (t) - анализируемая функция, g(At, t -t) - функция, достигающая максимума в точке t = т (в центре окна) и быстро спадающая до нуля за

пределами интервала

At At