Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 [ 8 ] 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121

Различается детерминированный хаос в консервативных системах, в которых механическая энергия (или какой-либо ее аналог) сохраняется, и в диссипативных системах (системах с «трением»). Мы в дальнейшем будем рассматривать в основном диссипативные системы.

Выявление и анализ детерминированного хаоса оказывается весьма полезным при управлении сложными движениями в самоорганизующихся системах.

Во-первых, если в некоторой динамической системе диагностируется динамический хаос, то можно надеяться, что некоторым изменением параметров (настройкой) можно упорядочить ее движение.

Во-вторых, переход от детерминированного к хаотическому движению происходит по некоторым универсальным сценариям, число которых невелико. Информация об этих сценариях может быть использована для назначения режимов работы, исключающих возникновение хаотических колебаний.

В-третьих, в современной теории нелинейных динамических систем развиты новые методы количественного анализа хаотических колебаний, которые с успехом могут быть использованы для идентификации характера движения и состояния объектов управления.

Возникновение хаотических движений в детерминированных системах возможно, если траектории движения обнаруживают сильную зависимость от начальных условий (траектории «разбегаются»). Впервые на это при изучении неинтегрируемых движений трех тел обратил внимание А. Пуанкаре (H. Poincare, 1892 г.), который писал: «...иногда небольшая разница в первоначальном состоянии вызывает большое различие в окончательном явлении. Небольшая погрешность в первом вызвала бы огромную ошибку в последнем. Предсказание становится невозможным... » Подобные идеи о возможности проявления хаотических движений в детерминированных системах высказывались также Биркгофом (G. D. Birkhoff, 1935 г.).

Таким образом, детерминированный хаос проявляется в том случае, когда задача Коши для уравнений движения является некорректно поставленной.

Напомним, что математическая задача называется корректно поставленной, если:

1) ее решение существует;

2) оно единственно;

3) решение устойчиво относительно малых изменений исходных данных (т. е. малые изменения исходных данных ведут к малому изменению решения).

Из предыдущего ясно, что возникновение детерминированного хаоса связано с нарушением третьего условия (условия устойчивости).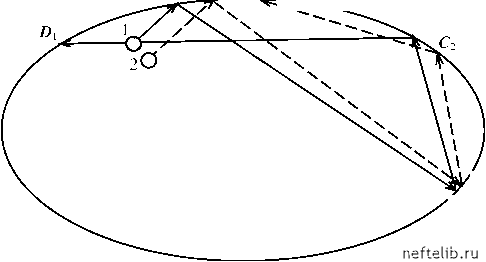

Рис. 1.7. «Разбегание» траекторий бильярдного шара

Приведем еще один простой пример, иллюстрирующий нарушение устойчивости.

Пусть последовательность задается следующей рекуррентной формулой

xn+1 = 1 - 2 xn , n = 0,1,2,... Рассмотрим поведение получаемых по этой формуле последовательностей в зависимости от начальной точки x0 из отрезка [0,1].

Возьмем сначала в качестве десятичные числа с одним знаком после запятой. Так, например, для Х0 = 0,1 получим = 0,8, = -0,6, Х3 = 0,2, Х4 =-0,6, Х5 = 0,2 и т. д., то есть последовательность вышла на предельный цикл из двух чисел.

Простейшая механическая система, в которой наблюдается «разбе-гание» траекторий, представляет собой бильярдный шар, ударяющийся и упруго отскакивающий от сторон эллиптического бильярдного стола (рис. 1.7).

Если начальное положение шара (1) чуть-чуть изменится (положение 2), то уже через несколько соударений шар будет двигаться по совершенно другой траектории. Эта неустойчивость приводит к тому, что при сохранении энергии для столов определенной формы шар случайно блуждает по столу, никогда не повторяя свою траекторию.

Известным литературным примером, иллюстрирующим сильную зависимость эволюции системы от начальных условий, является научно-фантастический рассказ Р. Бредбери «... И грянул гром», в котором гибель бабочки, случайно раздавленной в прошлом путешественником во времени, так влияет на ход истории, что приводит к существенному изменению настоящего.

А1 А2 D2

" С1

1.2.1. Странный аттрактор

Эволюцию динамических систем удобно представить в геометрической форме, используя фазовое пространство. Рассмотрим, например, движение маятника с трением, описываемое системой уравнений

du x

m- = -mg - au,

dt l

. dt

где x - отклонение маятника от точки равновесия, m - масса маятника, a -коэффициент трения, u - скорость движения маятника, l - длина маятника, g - ускорение свободного падения.

На фазовой плоскости (x,u) движение маятника представляется в

виде спирали, наматывающейся на точку О (0, 0) (рис. 1.8, а). Эта точка как бы «притягивает» к себе все траектории движения, из каких бы точек они не исходили. Поэтому точка равновесия О (0, 0) называется аттрактором этой динамической системы (от слова attract - притягивать).

Аналогичная картина наблюдается для всех других чисел с одним знаком после запятой, кроме Х0 = 0,5. В этом случае получаем Х1 = 0, =-1, Х3 =-1, т. е. последовательность сходится.

Рассмотрим теперь в качестве числа с двумя знаками после запятой. Например, Х0 = 0,12. В этом случае последовательность выходит на

цикл, содержащий 10 чисел.

Расчеты показывают, что аналогичная картина будет наблюдаться для всех чисел, кроме 16 чисел вида 0,05x(i + 10(к -1)), i = 1,2,3,4,6,7, 8,9; j = 1, 2, и трех чисел вида 0,25 x к, к = 1, 2, 3.

Для чисел с тремя знаками после запятой имеем четыре варианта поведения траектории предельного цикла. К предыдущим 3 вариантам добавляется вариант, в предельном цикле которого 50 чисел.

Продолжая увеличивать число знаков после запятой в x0 , можно наблюдать дальнейшее усложнение динамики системы.

Этот пример наглядно показывает, что желание считать как можно с большей «точностью» может привести не только к бесполезной потере времени, но и к потере адекватности описания за счет перехода на траектории движения, радикально отличающиеся от истинных. Таким образом, при моделировании нелинейных систем необходимо особое внимание обращать на определение оптимальной сложности модели (см. по этому поводу также раздел 2.3 данной книги).