Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 [ 107 ] 108 109 110 111 112 113 114 115 116 117 118 119 120 121

Очевидно, что 0 < L < 1. М

0,8 0,6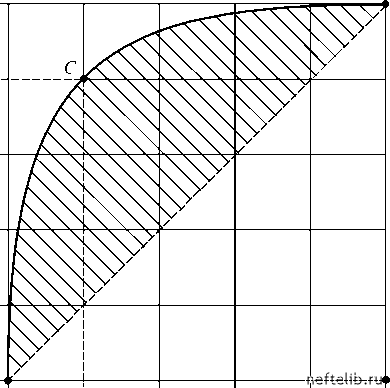

Рис. 5.19. Кривая Лоренца

Следует подчеркнуть, что коэффициент Лоренца определяется по интегрированным данным, поэтому эта величина устойчива к погрешности данных, что является общим свойством всех интегральных методов (см. раздел 2.1.3).

Ограничение в < 1, принятое нами, не является обязательным. Соотношения, подобные полученным выше, могут быть выведены и при в> 1, если считать выборку ограниченной (N <). Правда, полученные при этом формулы будут несколько сложнее.

5.4.2. Закон Парето в оценке запасов углеводородов

Начиная с работы Крига [28], было принято считать, что распределение запасов минеральных богатств, включая нефть и газ, подчиняется лог-нормальному закону. Однако в 1962 г. Б. Мандельброт показал, что это

распределение является гиперболическим [29] и в ранговом виде может быть выражено в виде

(5.58)

In r = In A -а In V,

где V - запасы природных ресурсов в месторождении, имеющем ранг r в упорядоченном (по убыванию запасов) множестве всех месторождений данного региона.

Таким образом, в двойных логарифмических координатах (in r - In V) мы получаем прямую, типичный вид которой представлен на рис. 5.20. Для месторождений нефти и газа обычные значения а лежат в интервале от 0,8 до 1,1 [29].

Гиперболичность распределения запасов объясняется тем, что расположение «ловушек» нефти и газа во многом определяется рельефом, а любой природный рельеф является масштабно-инвариантным. В распределении запасов проявляется и кластеризация. Например, некоторые регионы мира, такие Средний Восток или Западная Сибирь, содержат непропорциональные большие запасы нефти по сравнению с другими регионами. В то же время, распределение запасов в самих этих регионах также крайне неравномерно.

in r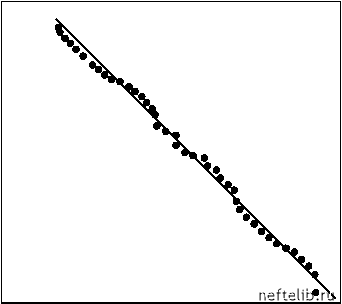

in V

Рис. 5.20. Зависимость ранга месторождения от величины запасов

Следует отметить, что гиперболическое распределение запасов становится явно видным только для хорошо разведанных регионов. Дело в том, что форма распределения разведенных запасов меняется по мере открытия новых месторождений (см. рис. 5.21). Как правило, вначале откры-

ваются наиболее крупные месторождения, а затем - все большее число мелких месторождений. По этой причине на ранней стадии распределение разведанных запасов напоминает логнормальное (см. кривую для момента времени t0 на рис. 5.21). Со временем, по мере увеличения числа открытий, кривая распределения все больше приближается к гиперболе. Правая ветвь кривой распределения меняется мало. Это означает, что после накопления достаточного объема информации закон Парето может быть использован для оценки объема запасов, оставшихся к какому-то моменту времени неоткрытыми. Линия AB на рис. 5.22 делит разведанные месторождения на две категории. Месторождения первой категории (справа от линии AB ) хорошо разведаны, поэтому они подчиняются закону в координатах In V - In r и ложатся на прямую CA . Месторождения второй категории (они расположены слева от прямой AB ) открыты на все, поэтому представляющие их точки отклоняются от прямой CA. Продолжив прямую CA, мы можем оценить величину неоткрытых еще запасов (область 3 на рис 5.22). Подчеркнем, что эта возможность неразрывно связана с масштабной инвариантностью иерархии запасов. Только то обстоятельство, что распределение мелких месторождений подобно распределению крупных, позволяет нам, «обучившись» на примере уже открытых месторождений, сделать обоснованный прогноз запасов еще неоткрытых месторождений. При этом закон Парето становится полезным инструментом количественной оценки величины неразведанных запасов.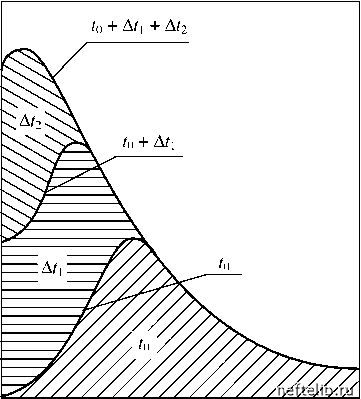

Размер месторождения Рис. 5.21. Распределение размеров разведанных месторождений