Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 [ 105 ] 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121

ко fH (s 0)~ 0,8, то оценка прироста дебита нефти может быть завышена на 20%-30%.

Полученные выше соотношения являются, по существу, уточнением формулы Фетковича [22], который предложил аппроксимировать функцию

a(Pr ) =

на интервале 0 < Pr < 1 (0 < P < PHac) линейной функцией, проходящей через начало координат (см. рис. 5.18, прямая 1), что, как легко видеть, также приводит к степенной зависимости H от Pr вида (5.42) с m = 2.

Согласно нашему подходу функция a(Pr) аппроксимируется зависимостью

a(Pr ) = fu (sг 0 )Pm-1, (5.50)

которая может быть получена путем дифференцирования (5.42) с учетом (5.46). Кривая 2 на рис. 5.18 представляет собой график функции (5.50) при f„ (s 0 ) = 0,8 и m = 1,8.

a(Pr)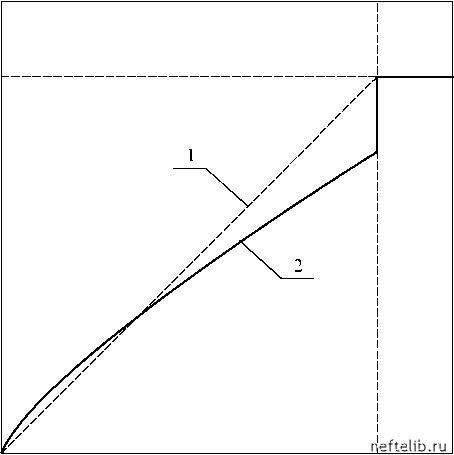

Рис. 5.18. Аппроксимации функции a(Pr ): 1 - аппроксимация Фетковича, 2 - формула (5.50) с fн (s 0) = 0,8 и m = 1,8

Как видим, основное отличие между этими зависимостями состоит в том, что аппроксимация Фетковича не учитывает скачка функции a(Pr) в

точке Pr = 1. Вместо этого снижение фазовой проницаемости нефти в зоне

разгазирования предлагалось учитывать путем введения в уравнения притока псевоскина [22]. Предложенный нами подход является более естественным.

Уравнение (5.49) можно переписать в виде

Q = K(Pr - Pc1),

P > P

c нас

Pc < P

Таким образом, в режиме локального разгазирования увеличение фильтрационных сопротивлений за счет выделения газа может быть учтено путем замены истинного значения забойного давления эффективным давлением Pc1. Оказывается [23], что при описании взаимодействия пласта

и скважины этот прием более удобен, чем общеизвестный подход, заключающийся в замене газированной жидкости однородной фазой с некоторой повышенной эффективной вязкостью [24].

5.4. Гиперболические законы распределения

Опыт реального применения методов математической статистики достаточно быстро убеждает в том, что информация о виде функции распределения совершенно необходима для получения надежных и практически полезных результатов. Так, в разделе 5.1 мы показали, что значение закона распределения случайной величины позволяет (при наличии компаратора) восстановить недостающие замеры с помощью процедуры безэталонных измерений. Но даже при наличии эталонов объем и качество имеющихся данных, как правило, таковы, что обоснованное определение одновременно вида функции распределения и ее параметров не предоставляется возможным. В такой ситуации рекомендуется применять непараметрические статистики, но за отказ от знания вида закона распределения приходится платить некоторой расплывчатостью ответов, получаемых непараметрическими методами. Таким образом, вопрос о виде функции распределения является одной из важнейших проблем практической статистики.

Принято считать, что универсальными законами распределения, которым подчиняется большинство случайных величин в природе, являются

нормальный и логнормальный законы. Некоторое теоретическое обоснование этому убеждению дает центральная предельная теорема, но часто нормальная функция распределения используется только в силу удобства и привычности.

Б. Мандельброт показал, что не менее универсальным законом распределения является гиперболический [25]. Гиперболические (степенные) законы распределения являются ближайшими «родственниками» фракталов - с этим и связана их широкая распространенность (мы уже упоминали об этом в главе 1).

5.4.1. Формы представления и свойства гиперболических зависимостей

Случайная величина X называется гиберполически распределенной,

если

Р(Х >x) = a, 0<x<oo, (5.51)

где Р(Х > х) - вероятность того, что X > x, A, a - некоторые постоянные положительные величины.

Если случайная величина дискретна, то вместо (5.51) используется соотношение

Nr (Х > х) = -, (5.52)

где Nr (Х > х) - общее число случаев, в которых (Х > х).

Предположив, что дискретные значения X ранжированы в порядке убывания, получим

Nr (Х > x(r ))= r, где x(r) - значения x, имеющие ранг r . Тогда, обращая (5.52), получим

x(r )= , (5.53)

где В = A1/a, в = 1/a.

Это соотношение позволяет оценить значение случайной величины по ее рангу, т. е. оказывается еще одним примером применения порядковых статистик (см. раздел 5.1).

Гиперболическое распределение, представленное в виде (5.51)-(5.52) называют законом Парето, в честь итальянского экономиста Вильфредо Парето, обнаружившего, что количество людей с доходом, превышающим некоторую величину x, уменьшается с ростом x гиперболически.

Дискретный закон распределения в форме (5.53) впервые ввел Джордж Ципф для описания частоты употребления в текстах слов различ-