Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 [ 62 ] 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121

Затем строят график ln(ko - k - ) от t и, повторяя те же операции, оценивают величины (A-1,Ядг-1), (A-2,Ядг-2) и т. д.

Для иллюстрации на рис. 3.3 показаны типичная кривая набухания и результаты ее обработки по одно- и многоэкспоненциальной зависимостям. Как видим, последняя модель весьма хорошо описывает кривые набухания глин. В табл. 3.1 приведены значения Ai, Я, полученные при обработке кривых набухания глины в различных растворах.

0,5 -

0,4 -

0,3 -

0,2 -0,1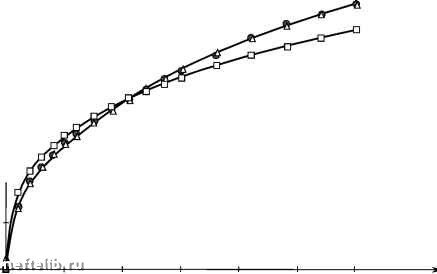

0 100 200 300 400 500 600 Время, с

-•- эксперимент ни- одноэкспоненциальная зависимость

-Ь- многоэкспоненциальная зависимость

Рис. 3.3. Корреляция между экспериментальными и расчетными данными о кинетике набухания бентонитовой глины

На рис. 3.4 приведены зависимости 1пЯ от номера уровня i. Как видим, эти зависимости могут быть описаны линейным уравнением

In Я = a + bi,

откуда

Я = Я)mi,

где Я0 = ea, m = eb.

Таблица 3.1

Результаты обработки кривых набухания бентонита

Отсюда следует, что иерархия времен {Я} масштабно-инвариантна (т. е. фрактальна), поскольку, как легко видеть,

= m = const.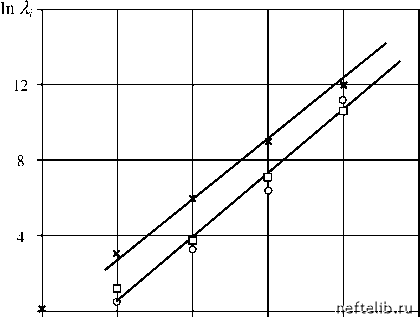

Рис. 3.4. Зависимость логарифма характерного времени набухания от номера уровня

о - пластовая вода; □ - водопроводная вода; х - полиглицерин 0,5%

3.4. Моделирование нестационарной фильтрации в пластах с фрактальной структурой

Традиционно пласт с ухудшенной проницаемостью описывается при помощи модели, состоящей из двух различных пространственно одно-

родных зон: «загрязненной» призабойной зоны и расположенной за ней зоны с большей проницаемостью. В ряде случаев эта несколько схематичная модель может быть уточнена за счет принятия некоторых дополнительных предположений о структуре пласта с ухудшенной проницаемостью. В условиях, когда какие-либо теоретические или экспериментальные исследования структуры «загрязненного» пласта отсутствуют, полезную информацию могут дать некоторые положения теории организации сложных систем. Так, можно ожидать, что зоны пласта с ухудшенной проницаемостью обладают, как и многие другие системы с неупорядоченной структурой, фрактальными свойствами (см. главу 1). Для примера на рис. 3.5 схематически изображен загрязненный пласт в рамках зонально неоднородной (а) и фрактальной (б) моделей.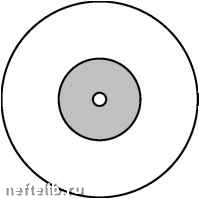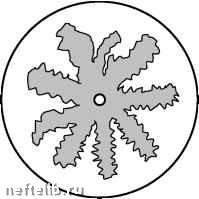

а) б)

Рис. 3.5. Модели неоднородного пласта

Подчеркнем, что речь здесь идет о пористых средах с крупномасштабной фрактальной структурой. Этот термин введен нами для того, чтобы подчеркнуть отличие последних от мелкомасштабных фрактальных структур теории протекания [22, 31, 32] и подразумевает выполнение неравенства

» l,

где l - характерный масштаб изменения градиента давления, - длина

корреляции. (Реальная система с фрактальными свойствами на масштабах, больших , является однородной. Грубо говоря, ее можно представить себе

как состоящую из фрактальных блоков размерами .)

Причины, которые приводят к образованию крупномасштабных фрактальных структур в изначально однородной пористой среде, весьма разнообразны. Практически все механизмы необратимого роста, рассматриваемые в литературе [22, 32], могут проявить себя в процессах нефтегазодобычи. Так, известно, что фракталы могут образовываться вязкими