Главная  Переработка нефти и газа 

Скача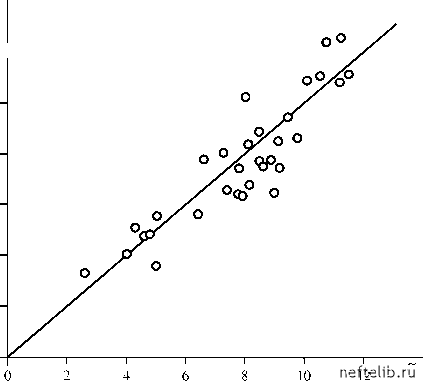ть эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 [ 54 ] 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121

-пр, МПа

-пр, МПа

Рис. 2.17. Зависимость расчетного давления на приеме насоса от фактического давления

2.9.4. Исследования скважин, оборудованных насосами с датчиками давления и регуляторами подачи

Описанные выше алгоритмы могут быть использованы при интерпретации данных исследования скважин с помощью ЭЦН, оборудованных датчиками давления на приеме и регуляторами скорости вращения двигателя. Определяя дебит на различных режимах работы насоса и одновременно замеряя динамический уровень и давление на приеме, можно рассчитать значения забойного давления и, тем самым, получить расчетную индикаторную кривую.

В этом случае предлагается следующий алгоритм интерпретации результатов. Возможны следующие варианты.

1. УЭЦН оборудованы датчиками давлений, что позволяет замерять давление на приеме Рпр. Тогда, интегрируя уравнение (2.88) по схеме

«сверху-вниз» на каждом режиме, определяют давление на приеме насоса Рпр при известном затрубном давлении. Затем из сопоставления расчетных и фактических значений Рпр корректируют эмпирические коэффициенты. Интегрируя уравнение (2.87) по схеме «сверху-вниз», на каждом ре-

жиме определяют забойное давление при известном давлении на приеме. Зная значения на каждом режиме, строят индикаторную кри-

вую P3 = P3 (Q).

2. ЭЦН не оборудованы датчиками давления. В этом случае на каждом режиме работы ЭЦН проводят опыты по закрытию затрубной задвижки и определяют скорость роста давления F и динамический уровень Hд.

По значениям F и Hд оценивается забойное давление. Проделав эти вычисления для всех режимов работы ЭЦН, строят индикаторную кривую.

Библиографический список к главе 2

1. Турчин В. Ф., Козлов В. П., Малкевич М. С. Использование методов математической статистики для решения некорректных задач УФН. -

1970. - Т. 102, № 3.

2. Успенский А. Б. Обратные задачи математической физики - анализ и планирование экспериментов Математические методы планирования эксперимента. - Новосибирск: Наука, 1981.

3. Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа. - М.: Наука, 1981.

4. Тихонов А. Н., Иванов В. К., Лаврентьев М. М. Некорректно поставленные задачи Дифференциальные уравнения с частными производными. - М.: Наука, 1970. - 407 с.

5. Тихонов А. Н., Арсенин В. Я. Методы решения некорректных задач. -М.: Наука, 1974. - 224 с.

6. Лаврентьев М. М., Романов В. Г., Шишатский С. П. Некорректные задачи математической физики и анализа. - М.: Наука, 1980. - 286 с.

7. Федоров В. В. Активные регрессионные эксперименты Математические методы планирования эксперимента. - Новосибирск: Наука, 1981.

8. Химмельблау Д. Анализ процессов статистическими методами. - М.: Мир, 1973. - 958 с.

9. Успенский А. Б., Федоров В. В. Вычислительные аспекты метода наименьших квадратов при анализе и планировании регрессионных экспериментов. - М.: Изд-во МГУ, 1975. - С. 122-140.

10. Цыпкин Я. З. Адаптация, обучение и самообучение в автоматических системах Автоматика и телемеханика. - 1966. - № 1.

11. Петров Б. Н., Крутько П. Д. Применение теории чувствительности в задачах автоматического управления Изв. АН СССР. Сер. Техническая кибернетика. - 1970. - № 2. - С. 300-305.

12. Розенвассер Е. Н., Юсупов Р. М. Чувствительность систем управления. - М.: Наука, 1981. - 464 с.

13. Живоглядов В. П., Каипов В. Х. О применении метода стохастических аппроксимаций к проблеме идентификации Автоматика и телемеханика. - 1966. - № 10. - С. 54-60.

14. Георгиевский В. Б. Унифицированные алгоритмы для определения фильтрационных параметров. Справочник. - Киев: Наукова думка,

1971. - 328 с.

15. Блехман И. И., Мышкис А. Д., Пановко Я. Г. Механика и прикладная математика. Логика и особенности приложения математики. - М.: Наука, 1983. - 328 с.

16. Вапник В. Н. Восстановление зависимостей по эмпирическим данным. -М.: Наука, 1979. - 448 с.