Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 [ 86 ] 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121

рости (v~ 0,04 м/с) пропускная способность после начала прокачки газожидкостной системы монотонным образом увеличивается до некоторого нового стационарного значения (см. рис. 4.20, б).

Дальнейшее уменьшение скорости течения (v < 0,02 м/с) приводит к тому, что изменение пропускной способности принимает колебательный характер. Поскольку характерные времена изменения пропускной способности намного больше времени прохождения частицами газожидкостной системы трубы t0, то можно предположить, что колебания пропускной способности связаны с накоплением зародышей газа в пристенных областях трубы и их последующим выносом.

6,38

5,74

6,38

кг с - Па

5,74

6,38

5,74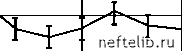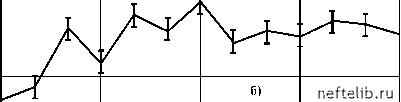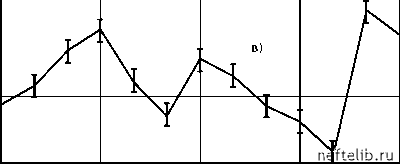

t, мин

Рис. 4.20. Зависимость k = k (t)

F (N1 ) =

J , (4.10)

где в, М, s - некоторые постоянные (s > 1). При N1 >[(s - 1)М]-1 s функция (4.10) монотонно убывает, что объясняется уменьшением интенсивности образования крупных зародышей при больших N1 из-за наличия пространственных ограничений.

Расход жидкости в условиях описанного выше эксперимента находится из уравнений

G = K (р1 - р2 ),

Для описания этих процессов рассмотрим следующую эвристическую модель. Предположим, что в пристенных областях трубы скапливаются зародыши газа двух видов - «мелкие» и «крупные», радиусами R1 и 2 соответственно. Зародыши радиуса 1 первоначально находятся в объеме жидкости и осаждаются на стенках при протекании жидкости по трубе. Центрами осаждения зародышей радиуса 1 являются зародыши радиуса R2, поэтому скорость осаждения мелких зародышей пропорциональна численности крупных зародышей. Будем считать, что в дальнейшем часть мелких зародышей с какой-то скоростью покидает стенки трубы. Взаимодействие оставшихся мелких зародышей со стенками трубы нарушает их стабильность, и они постепенно растут за счет диффузионного притока молекул газа из объема жидкости, достигая за некоторое время т размеров крупных зародышей. Зародыши радиуса R2, взаимодействуя с потоком жидкости, изменяют гидродинамическую обстановку в пристенных областях, что увеличивает пропускную способность трубы. Будем считать, что крупные зародыши могут быть вынесены потоком жидкости, поэтому скорость их уменьшения пропорциональна расходу G.

Сделанные выше предположения приводят к следующей системе дифференциальных уравнений с запаздывающим аргументом, описывающей процессы накопления и выноса зародышей:

dN- = oN 2 - F (N1(t - т))

N , (4.9)

dN2 = -dGN 2 + F (N1(t - т)\ dt

где N1 и N2 - численности мелких и крупных зародышей на стенках трубы; а и у- коэффициенты, характеризующие скорости, с которыми мелкие зародыши осаждаются на стенках и покидают их; д - коэффициент, характеризующий скорость выноса крупных зародышей; F(N1) - функция, определяющая интенсивность образования крупных зародышей из мелких. Зададим следующую параметризацию функции F(N1):

v = aN 20

- , л 7

rN1 r

1 + C

Анализ показывает, что при r = vA - g < 1 система (4.13) имеет единственное состояние равновесия - точку О (0, 0). При r > 1 существует

где p1 - давление на входе трубы, p2 - давление в конце трубы перед краном, p0 - давление после крана (атмосферное давление), С - коэффициент, характеризующий сопротивление крана. Исключив p2, получим,

G = (4.11)

- + C K

где Аpo = p1 - p0 - постоянный в условиях опыта перепад давления. Как

уже отмечалось, пропускная способность трубки при наличии зародышей увеличивается, причем относительное изменение достигает 10%. Поэтому зависимость K от N2 можно параметризовать в виде

K = K, (4.12)

1 - mn 2

где m > 0 и величина м N2 мала. Подставив (4.10)-(4.12) в (4.9), получим после обезразмеривания

dt 1 + (t - т)

dt 1 - П2 1 + (t - t)

где ni = (i = 1,2),

Ni 0

N10 = M-Vs, N20 = 1+CK0,

t t 1

t , t -, t0 =-,

t0 t0 r