Главная  Переработка нефти и газа 

Ск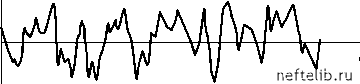ачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 [ 74 ] 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121

P(t)

Рис. 3.17. Пульсации давления в скважине:

а) - м 1,0 мПа-с; б) - м 50 мПа-с; в) - м 540 мПа-с

Степень нерегулярности (хаотичности) изменения давления P в трубах можно оценить по размерности Хаусдорфа D для графика зависимости Р = P(t) (см. раздел 3.5 и главу 1). Для кривых a) и б) на рис. 3.17 получены значения D = 1,31 и D = 1,15 соответственно. Аппроксимируя зависимость D от логарифма M прямой линией, получим (рис. 3.18), что при D = 1 величина м> 0,58 Па-с. Эта величина соответствует вязкости эмульсии в НКТ, для которой получена кривая в) (третья точка на

рис. 3.18).

Более глубокий анализ может быть произведен с помощью вычисления корреляционной размерности V (см. раздел 1.4).

На рис. 3.19 приведена зависимость корреляционного интеграла lnC(е) от lne, полученная для кривой а) из рис. 3.17 при m = 2. На рис. 3.20 приведена зависимость vm = vm (m) для этой же кривой. Вид этой

кривой (рост с насыщением) свидетельствует о том, что случайные пульсации давления имеют детерминированную основу.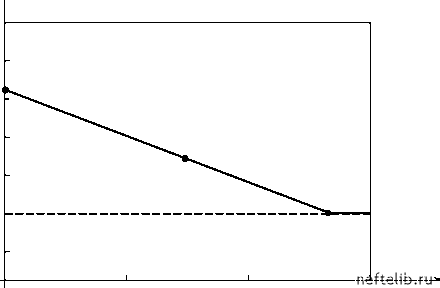

M, мПа • с

Рис. 3.18. Зависимость размерности Хаусдорфа от вязкости жидкости в НКТ

ln C(e)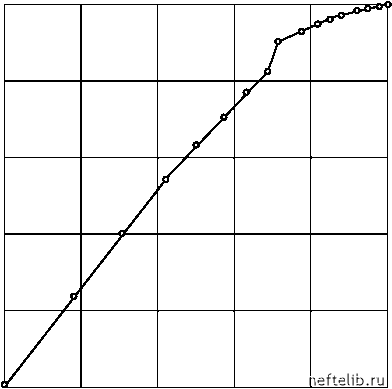

1,2 1,7 2,1 ln e-

Рис. 3.19. Зависимость lnC от lne при m = 2

Область применения размерностных характеристик не ограничивается определением того, каким является источник случайных сигналов - шумовым или детерминированным. Более ценным является использование размерностей D и v для диагностирования режимов работы насоса (утечки, заклинивания, рост динамических составляющих нагрузок на колонну и т. д.).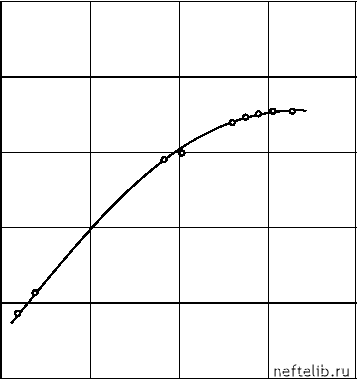

Рис. 3.20. Зависимость vm от m

Поскольку предельное значение корреляционной размерности v ~ 3,6, то минимальное число динамических переменных, необходимое для моделирования работы штангового насоса, равно [3, 6] +1 = 4.

Следовательно, сосредоточенная динамическая модель ШГН должна представлять собой систему из четырех уравнений. Из физических соображений ясно, что эти уравнения должны учесть инерцию и упругость колонны штанг, а также инерцию и сжимаемость жидкости.

Уравнение колебания штанг можно записать в виде

M- = Fc + + K- X) - /плП(и)(Ртр - Рпр) -

(3.98)

где X - перемещение плунжера; - перемещение точки подвеса колонны штанг; M - масса колонны штанг;