
 |
|
|
Главная Переработка нефти и газа Таким образом, величина At имеет смысл ширины окна. Результаты оконного преобразования Фурье удобно представлять на плоскости время-частота (см. рис. 1.22, а). На рисунке 1.22 вертикальные линии указывают границы окон, а горизонтальные - различные значения частоты. Образованные этими линиями прямоугольники соответствуют гармоникам определенной частоты со, локализованным с помощью окна с определенным центром t = т. Степень корреляции анализируемого сигнала с такими локализованными гармониками (определяемую коэффициентами разложения F{о),т)) отображают путем закрашивания прямоугольников в различные цвета (чем меньше значение F{со,т), тем темнее цвет). Для сравнения, на рис. 1.22, б представлены результаты простого (не оконного) Фурье-преобразования в проекции на ту же плоскость т-с. Как видим, это преобразование хорошо локализует частоту, но не позволяет получить временное разрешение. Рис. 1.22. Частотно-временная локализация преобразований а) - оконное преобразование Фурье; б) - простое преобразование Фурье; в) - вейвлет-преобразование. Оконное преобразование Фурье локализует анализ, но не учитывает то обстоятельство, что реальные сигналы обычно представляют собой сумму составляющих, частота которых тем больше, чем меньше их продолжительность. Вследствие этого высокочастотная информация должна быть извлечена из относительно малых интервалов времени, а низкочастотная информация добывается на более продолжительных отрезках времени [40]. Иными словами, ширина окна должна уменьшаться с увеличением частоты, что для оконного преобразования Фурье не выполняется (см. рис. 1.22, а и сравните с рис. 1.22, в). Конечно, при практическом применении Фурье-анализа все упомянутые выше нюансы в той или иной мере учитывались путем проведения различных экспериментов с окнами переменной ширины. Наконец, эта (зачастую интуитивная) деятельность привела, вместе с осознанием масштабной инвариантности природных процессов, к появлению формализованного аппарата вейвлет-анализа. Интегральное вейвлет-преобразование функции f(t )записывается в виде [40] W (s,t)= \f (t )YsT(t )dt, где y/sT(t) - вейвлет-функции, полученные из некоторого материнского вейвлета 0 (t) растяжением по горизонтали в s раз, сжатием по вертикали в VS раз и сдвигом по оси времени на отрезок т: () 1 (t Wsrit) = -г0 - . Обратное вейвлет-преобразование имеет вид [40] () 1 0 0 (t-тЛ ()dsdт C-Оо-Оо V s J s2 где C - нормализующий коэффициент, 0 2 -1 C = \ y/(a) a da< о , где y/0(a) - Фурье-образ функции 0(t). Вейвлеты представляют собой всплески, образованные несколькими осцилляциями, быстро спадающими до нуля за пределами базового интервала. В табл. 1.2 приведены наиболее часто употребляемые вейвлеты. Отметим, что первые два вейвлета комплекснозначны, и на рисунках изображены их вещественные и мнимые (штриховые линии) части. Основные признаки вейвлет-функции: она должна быть ограничена: и иметь нулевое среднее: V0(t )dt = 0. Часто для подавления медленно меняющихся составляющих сигнала f {t) требуют равенства нулю не только нулевого, но и нескольких первых моментов: tmY0 {t )dt = 0, m = 1,2,... Полная энергия сигнала может быть записана через амплитуды вейв-лет-преобразования в виде [40] oo I* f,..2, E{f )= If 2 {t)dt = C IJw2 {.,т) dsdт Таблица 1.2 Основные типы вейвлетов 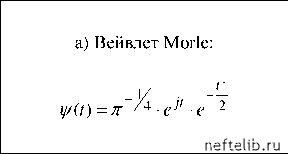 0,0 -0,3 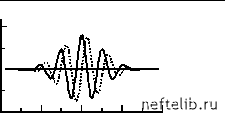 -4 -2 0 2 4 б) Вейвлет Paul: (t) = {1 - it) -0,3 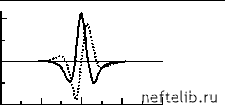 -4 -2 0 2 4 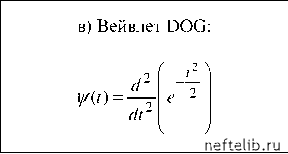 0,3 - -0,3  -4 -2 0 2 4 - сю - сю 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 [ 21 ] 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 |
||
 |
 |