Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 [ 56 ] 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121

Согласно этому соотношению, Ma Ms при 1 . Следовательно,

функция Ms определяет равновесное (стационарное) значение вязкости, соответствующее данному значению j&. Поскольку уже при t > 3Я

/Я 0, то величина Я(у) имеет смысл характерного времени установления равновесия.

Обобщением (3.2) является нелинейное кинетическое уравнение, предложенное Денни и Бродки (D. A. Denny, R. S. Brodkey, 1962 г.) [1]:

dг = k1 (1 - s f - k2sm, (3.5)

Последовательное развитие этих представлений с использованием подходов, разработанных в теории химических реакций, приводит к кинетическим уравнениям вида

-г = f (s,r), (3.1)

моделирующим нестационарные процессы в неньютоновских средах. Эффективная вязкость материалов pa считается некоторой функцией величины s, требующей специального задания: jUa = pa (s).

Простейшее линейное уравнение вида (3.1) можно записать по аналогии с кинетическим уравнением первого порядка:

--- = ki(i&)si -k2(:r)s, (3.2)

где ki = ki(}&) и 2 = 2(;) - константы скоростей «реакций» разрушения и восстановления связей, в общем случае зависящие от скорости сдвига ]&.

Зависимость pa = Ma (s) в линейном приближении может быть задана соотношением

Ma =Mo -(Mo -Moo)s . (3.3)

Согласно (3.3) при s = 0 (неразрушенная структура) M = M0, а при s = 1 (полностью разрушенная структура) Ma = Moo. Из (3.2) и (3.3) легко получить уравнение

Я(г) + Ma =Ms (Y), (3.4)

где Л()&) =-, Ms= Mo-M7-kV, M = Mo-Moo.

Решение (3.4) с начальным условием Ma (0) = Mo имеет (при i& = const) вид

l0-la

(3.6)

Соотношение в неявном виде определяет равновесную зависимость кажущейся вязкости от скорости сдвига = iia ("у). Существенным недостатком подобных теорий является наличие большого числа констант, не поддающихся теоретической оценке, поэтому они вряд ли могут быть использованы для непосредственного описания экспериментальных данных. Модели такого рода предназначены, скорее, для выявления качественных особенностей нестационарных процессов в реологически сложных средах.

Рассмотрим некоторые возможные пути уточнения кинетических моделей неньютоновских сред.

Как известно, скорость диссипации механической энергии в единице

объема жидкости равна W = laY& . Естественно предположить, что часть

этой энергии тратится на разрушение структурных связей, поэтому константу скорости разрушения k1 можно считать функцией величины W. Это

позволяет уточнить вид зависимости k1 от скорости сдвига:

k1 = k1 (s )]&2 ).

Повреждения пространственной «сетки» могут служить центрами, в окрестностях которых процессы деструкции резко ускоряются («где тонко, там и рвется»), поэтому константу скорости разрушения структуры можно считать возрастающей функцией концентрации разрушенных связей s.

Приведенные выше соображения можно учесть, например, в следующем кинетическом уравнении:

d -k2S + kola (s)y&2s(1 - s), (3.7)

где k0 - некоторая постоянная.

Эффективная вязкость сильнее всего меняется также на начальной стадии разрушения структуры, поэтому линейная связь (3.3) качественно

где n и m - постоянные, аналогичные стехиометрическим коэффициентам, используемым в химической кинетике.

В теории Денни и Бродки принимается, что 2 = const, а константа скорости разрушения является возрастаюшей функцией скорости сдвига:

k1 = koYp.

Предполагается также, что эффективная вязкость определяется соотношением (3.3).

При достаточно продолжительном деформировании с постоянной скоростью сдвига "у устанавливается равновесное состояние, определяемое

условием - = 0, которое можно, используя (3.3) и (3.5), переписать в виде dt

неверна. Вместо нее целесообразно использовать экспоненциальные зависимости вида

Ma (s) = Moo+(m0 -Moo)exp

(3.8)

Здесь величина s0 определяет область, в которой эффективная вязкость меняется наиболее значительно (рис. 3.1).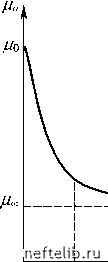

Рис. 3.1. Зависимость эффективной вязкости от концентрации

разрушенных связей

Для описания нестационарных процессов в реопектических средах (характеризующихся образованием структурных связей под действием деформаций) может быть предложено кинетическое уравнение

dq dt

k2 qY - k1qmf Y.

(3.9)

где q - концентрация структурных связей, образовавшихся в результате сдвиговых деформаций, k1 и k2 - константы скоростей разрушения и восстановления связей, m - порядок «реакции» разрушения структуры.

Согласно (3.9) при малых имеет место структурообразование, интенсивность которого пропорциональна скорости сдвига. С увеличением

второй член в правой части (3.9) начинает превышать первый, т. е. процессы разрушения структуры превалируют над процессами структурообразо-вания. Это вполне согласуется с тем, что реопектические эффекты на практике наблюдаются лишь при достаточно малых скоростях сдвига. Из (3.9) следует, что скорость структурообразования пропорциональна концентрации структурных связей. Это связано с предположением о том, что уже существующие связи служат центрами, ускоряющими образование новых,