Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 [ 30 ] 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121

л (i+1) -

в = yi , (2.14)

л(i+1)

где в - оценка параметра в, полученная после (1+1)-го замера.

Легко показать, что предложенный алгоритм неустойчив. Действительно, по формуле Тейлора, имеем

u (ti+1 ) = u (ti) + u Xti )At + u "(ti + o(At )2,

откуда

At i At i 2

Для относительной погрешности определения производной u(ti) получим выражение

= вг

Su esu < в

2£ , ,„A u

At 2

(2.15)

u 1 - u 1 - u

где £ - абсолютная ошибка величины u.

Так как в первом слагаемом правой части (2.15) величина At стоит в знаменателе, то ясно, что при малых At дифференцирование экспериментальных функций является неустойчивой операцией: малые погрешности £ приводят к большим ошибкам в определении u .

Процедуру вычисления u можно регуляризовать, увеличивая промежуток времени между замерами At. Однако при этом увеличивается ошибка, допускаемая при конечно-разностной аппроксимации производной.

Минимальная ошибка, согласно (2.15), достигается при 2£= u"

A 2

или At = 2

£ . Su в

При таком значении At -;- ~-

u u 1 - u

Рассмотрим следующий математический эксперимент. В качестве замеров yi возьмем «зашумленные» значения решения уравнения (2.13)

при в=1 и начальном условии u(0) = 0:

y. = 1 - e-i + £i, £ < 0,01, (2.16)

Требуется определить параметр в по замерам yi = u (ti ) + £, произведенным в дискретные моменты времени ti = iAt (i = 1,2,...,l). Заменяя

„ du Vi+1 - Vi

производную конечно-разностной аппроксимацией - ~---, полу-

dt At

чим из (2.13)

в =(1 - У> )At

и используем их для оценки величины в по формуле (2.14). Считая u ~ 0,5,

= e-1 ~ 0,5, получим, что оптимальное значение At в этих условиях равно 0,2. На рис. 2.1. приведены оценки величины в для разных моментов времени при At =0,02 и At =0,2 (см. рис. 2.1, а и б соответственно).

0,5 в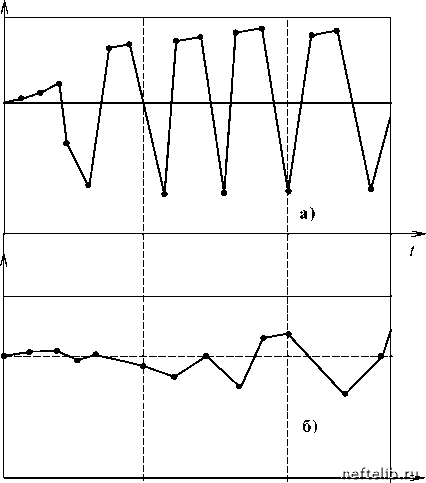

Рис. 2.1. Оценки величины в для разных моментов времени

при At =0,02 и At =0,2

Как видим, при At =0,02 проявляется неустойчивость решения обратной задачи. Увеличение промежутка времени между замерами до At =0,2 устраняет неустойчивость при t < 1, но приводит к смещению оценки на 10%. При t > 1 неустойчивость появляется за счет уменьшения величины 1-u.

Операция интегрирования, являясь обратной операции дифференцирования, в отношении воздействия на погрешности обладает также противоположными свойствами: при интегрировании погрешности экспериментальных функций сглаживаются. В ряде случаев, подвергая дифференциальное уравнение различным интегральным преобразованиям, можно получить выражения, в которых будут отсутствовать производные экспери-

(1 - u )dt

Подставив вместо значений u(ti ) замеры yi и произведя численное интегрирование, получим оценку

л yl - y1

в= l l -. (2.18)

AtxT1 - yi + yi+1

il 2 ,

В выражении (2.17) отсутствуют производные экспериментальной функции, поэтому (2.18) дает достаточно точный результат. Так, использование данных математического эксперимента (2.16) при At =0,02 и l = 10

приводит к оценке в , отличающейся от истинного значения в=1 не более чем на 0,3%.

2.1.4. Применение нреобразования Лапласа при решении обратных задач

Если алгоритм определения параметров линейной модели связан с получением точного решения прямой задачи, то целесообразно осуществить преобразование Лапласа по следующим трем причинам.

1. Как правило, аналитическое решение модели проще получить в пространстве изображений, чем во временной области.

2. Преобразование Лапласа является интегральным преобразованием, что приводит к сглаживанию погрешностей экспериментальных функций.

3. Часто, исходя из точного решения в изображениях, удается получить асимптотики при t - о и t - 0 решений во временной области и эффективно использовать их при решении обратных задач.

В связи с этим методы решения обратных задач, основанные на применении преобразования Лапласа, находят весьма широкое применение.

Эксперименты, предназначенные для определения параметров моделей, проводятся во временной области, поэтому для того, чтобы можно было осуществить оценивание, необходимо либо решение прямой задачи преобразовать ко времени t, либо экспериментальные данные о процессе перевести в пространство изображений по Лапласу. Ниже рассматриваются оба этих способа.

ментальных функций, что избавит от необходимости дифференцирования последних.

Так, проинтегрировав уравнение (2.13) по времени, получим

в= u(l) - u(t1). (2.17)